Пусть точка движется по координатной прямой и закон ее движения (координата точки в момент времени t) задается функцией 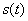 . В момент времени
. В момент времени 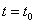 она находится в точке с координатой
она находится в точке с координатой 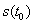 , а в момент времени
, а в момент времени 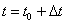 – в точке с координатой
– в точке с координатой 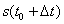 . Тогда перемещение точки за промежуток времени
. Тогда перемещение точки за промежуток времени 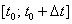 равно
равно 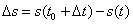 .
.
Величина 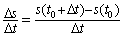 называется средней скоростью перемещения точки за промежуток времени
называется средней скоростью перемещения точки за промежуток времени 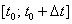 :
:
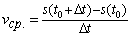 .
.
Предел средней скорости при 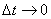 называется мгновенной скоростью точки в момент времени
называется мгновенной скоростью точки в момент времени 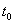 :
:
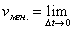
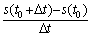 .
.
При прямолинейном движении, совершаемом по закону 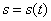 , мгновенная скорость точки в момент времени
, мгновенная скорость точки в момент времени 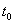 равна значению производной функции
равна значению производной функции 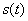 в точке
в точке 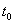 :
:
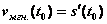 .
.
Аналогично определяется мгновенная скорость изменения других физических величин. Так, например, мгновенное ускорение (скорость изменения скорости) точки в момент времени 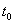 равно значению производной функции
равно значению производной функции 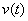 в точке
в точке 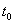 :
:
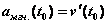
или
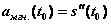
Пример 1. Материальная точка движется прямолинейно по закону 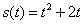
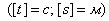 . Найдите мгновенную скорость точки в момент времени
. Найдите мгновенную скорость точки в момент времени 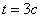 .
.
Решение.
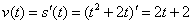
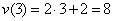
|
| Ответ: 8 м / c |
Пример 2. Материальная точка массой 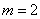 кг движется прямолинейно по закону
кг движется прямолинейно по закону 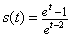
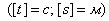 . Найдите кинетическую энергию точки в момент времени
. Найдите кинетическую энергию точки в момент времени 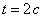 и равнодействующую всех сил, действующих на точку в этот момент.
и равнодействующую всех сил, действующих на точку в этот момент.
Решение.
Кинетическая энергия 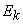 вычисляется по формуле вычисляется по формуле 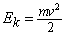 , а равнодействующая F всех сил, действующих на точку, по формуле , а равнодействующая F всех сил, действующих на точку, по формуле 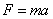 . .
|
а) 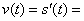 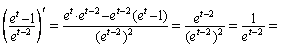 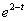 откуда
откуда 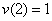 и, следовательно, и, следовательно, 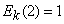 ; ;
|
б) 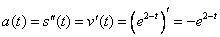 откуда
откуда 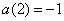 и и 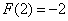
|
Ответ: 1 Дж; 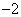 Н. Н.
|
 2015-07-14
2015-07-14 313
313








