Тест № 5 РЭЦ

(Расчет электрических цепей)

Вопрос	Ответ
№	Содержание	№	Содержание
	При последовательном включении источников ЭДС эквивалентная ЭДС находится как		произведение всех ЭДС.
	арифметическая сумма всех ЭДС.
	алгебраическая сумма всех ЭДС.
	сумма обратных величин.
	При последовательном включении двух источников ЭДС 15 и 10 В их эквивалентная ЭДС может быть равна		7,5 В.
	12,5 В.
	5 В.
	25 В.
	Мощность вырабатываемой источником питания электрической энергии определяется по формуле		Р = ЕU
	P = EI
	P = E/I
	P = UI
	Мощность отдаваемой источником питания электрической энергии определяется по формуле		Р = ЕU
	P = EI
	P = E/I
	P = UI
	Выражение I 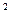Rявляется одним из вариантов математической записи закона		Джоуля – Ленца
	Ома
	Кирхгофа
	Кулона
	ВыражениеU/Iявляется одним из вариантов математической записи закона		Джоуля – Ленца
	Ома
	Кирхгофа
	Кулона
	Формула закона Ома для полной цепи имеет вид		U = E + Iro
	U = E – Irнагр.
	I = U/R
	U = E - Iro
	Если ток в цепи определяется выражением I = U/(R1 + R2 + R3), сопротивления R1, R2,иR3соединены		последовательно.
	параллельно.
	-
	-
	Если ток в цепи определяется выражением I = U (R1 + R2)/(R1 R2), то сопротивления R1иR2соединены		последовательно.
	параллельно.
	-
	-
	При параллельном соединении активных сопротивлений общая проводимость между двумя узлами равна		величине, обратной сумме сопротивлений всех ветвей.
	сумме проводимостей всех ветвей.
	сумме токов всех ветвей.
	сумме сопротивлений всех ветвей.
	Эквивалентное сопротивление трех сопротивлений по 24 Ом составляет 8 Ом при соединении их		параллельно.
	смешанно.
	последовательно.
	правильный ответ не дан.
	При параллельном соединении одинаковых по величине активных сопротивлений ток в неразветвленной части цепи		равен току через любое из сопротивлений.
	равен произведению тока через одно из сопротивлений на число сопротивлений.
	равен току через первое сопротивление.
	равен току через последнее сопротивление.
	Определить напряжение питания цепи, состоящей из трех сопротивлений величиной 1, 4 и 5 Ом, если ток через все сопротивления одинаков и равен 2 А.		10 В.
	20 В
	5 В
	0,2 В
	Первый закон Кирхгофа применяется для составления		узловых уравнений.
	контурных уравнений.
	уравнений контурных токов.
	для определения напряжения на зажимах источника питания.
	Второй закон Кирхгофа применяется		для узлов.
	для контуров.
	для ветвей.
	для определения напряжения на зажимах источника питания.
	Количество независимых узловых уравнений для цепи, имеющей пять узлов, равно		5.
	6.
	4.
	2.
	Количество независимых узловых уравнений для цепи, имеющей два независимых контура, равно		0.
	3.
	2.
	1.
	Сопротивление участка цепи из двух параллельно включенных одинаковых по величине сопротивлений после переключения их последовательно		увеличится в два раза.
	уменьшится в два раза..
	увеличится в четыре раза.
	уменьшится в четыре раза.
	Для определения электрических величин в одной из ветвей сложной электрической цепи наиболее удобен метод		суперпозиции.
	эквивалентного генератора.
	узловых и контурных уравнений.
	контурных токов.
	Ток цепи, состоящей из трех параллельно включенных сопротивлений величиной 2, 4 и 6 Ом, при напряжении питания цепи 12 В равен		4 А.
	2 А.
	1 А.
	11 А.
	При параллельном включении сопротивлений		нагрев всех сопротивлений одинаков.
	ток через большее сопротивление меньше.
	напряжение на большем сопротивлении больше.
	При параллельном включении сопротивлений		нагрев всех сопротивлений одинаков.
	нагрев большего сопротивления больше.
	напряжения на всех сопротивлениях равны.
	ток во всех сопротивлениях одинаков.
	Частичные токи необходимо находить при расчете электрических цепей методом		суперпозиции
	узловых потенциалов
	контурных токов
	эквивалентного генератора
	Если контурные токи двух соседних контуров направлены встречно, ток в общей ветви определяется как		сумма контурных токов
	произведение контурных токов.
	разность контурных токов
	частное от деления большего контурного тока на меньший контурный ток.
	Метод, при котором используются первый и второй законы Кирхгофа, называется методом		контурных уравнений.
	узловых и контурных уравнений.
	узловых потенциалов.
	суперпозиции.
	При методе расчета последовательным упрощением цепи (свертыванием ее) расчет сводится к определению электрических величин		по первому закону Кирхгофа.
	по второму закону Кирхгофа.
	по закону Джоуля-Ленца.
	по закону Ома.
	Проверка правильности расчета токов и напряжений в электрической цепи может быть выполнена		по уравнению баланса мощностей.
	по закону Ома.
	по закону Кулона.
	по закону полного тока.
	Используя закон Джоуля-Ленца, можно		найти напряжение на любом источнике питания цепи.
	найти ток любого источника питания цепи.
	найти ЭДС любого источника питания цепи.
	составить баланс мощностей цепи.
	При встречных направлениях тока и ЭДС источника питания он работает как		потребитель электроэнергии.
	источник электроэнергии.
	электрическая емкость.
	Правильный ответ не дан.
	Если ЭДС источника питания меньше напряжения на его зажимах, он работает как		потребитель электроэнергии.
	источник электроэнергии.
	электрическая емкость.
	Правильный ответ не дан.