Свойства функции распределения

1. Значения функции распределения принадлежат отрезку [0; 1]:

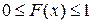
Вытекает из определения F(x) как вероятности

2. F(x) – неубывающая функция, т.е. если 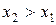, то .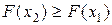

Док-во:

Рассмотрим на оси абсцисс две точки x₁ и x_2, причем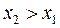

Событие, заключающееся в том, что случайная величина X примет значение меньшее x₂ можно разбить на два несовместных события

X < x₂: X < x₁ или x₁£ X <x₂

Значит P(X<x₂)=P(X<x₁)+P(x₁£X<x₂)

Тогда из (1) получаем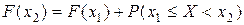

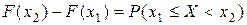(2)

Поскольку вероятность всегда ³0, то

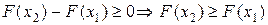, что и требовалось доказать.

Следствие 1. Вероятность попадания случайной величины на заданный промежуток.

Вероятность того, что случайная величина X примет значение, заключенное в интервале 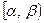равна

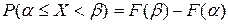(3)

Доказательство следует из (2), где .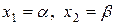

Следствие 2: Вероятность того, что непрерывная случайная величина X примет одно определенное значение равна нулю.

Док-во: (вероятность для каждого отдельного значения непрерывной случайной величины =0). В формуле (3) заменим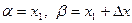

После: в формуле (3) заменим .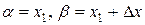

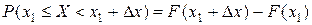устремим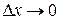

X – непрерывная случайная величина, F(x) – непрерывная функция, значит 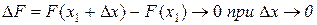. Тогда 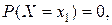что и требовалось доказать. Из следствий 1 и 2 получим:

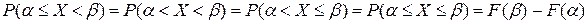(4)

Замечание. Ранее встречались с событиями, вероятность которых равна нулю. Это были невозможные события. Теперь доказали, что обладать нулевой вероятностью могут и возможные события: событие X=x ₁ (X принимает значение x₁) возможно, а его вероятность равна нулю. Такое возможно при испытаниях, не сводящихся к схеме случаев.

Аналог: тело имеет определенную массу, но ни одна из точек внутри тела определенной конечной массой не обладает. Вероятность попадания на сколь угодно малый участок не равна нулю, в строго определенную точку равна нулю.

3. Если возможные значения случайной величины X принадлежат интервалу (a, b), то

1. F(x)=0, при x £ a

2. F(x)=1, при x ³ b

Док-во.

1. x₁ £ a

F(x₁)=P(X<x₁)=0

2. x₂³ b

F(x₂)=P(X<x₂)=1

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси x, то

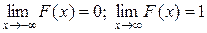
Вывод. Функция распределения F(x) любой случайной величины есть неубывающая функция, значения которой заключены между 0 и 1, т.е.0 £ F(x) £ 1, причем F(-¥) = 0; F(+¥)= 1.

Например:

Замечание. В некоторой литературе случайную величину X называют непрерывной, если ее функция распределения непрерывна и дифференцируема всюду, кроме, быть может, отдельных точек, где она терпит излом.