I. Математическое ожидание

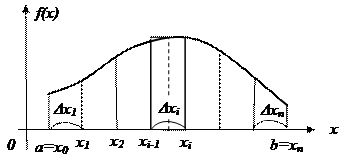
Пусть непрерывная случайная величина Х задана плотностью распределения f(x) и все ее возможные значения принадлежат отрезку [ a, b ]. Разобьем отрезок [ a, b ] на n частичных отрезков длиной 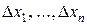. На каждом частичном отрезке выберем произвольную точку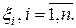

Для определения M(X) по аналогии с дискретной случайной величиной составим сумму произведений возможных значений 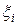на вероятности p_i попадания их в частичный интервал .

.

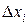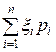Вероятность р_i равна площади частичной криволинейной трапеции с основанием 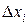и приближенно равна площади прямоугольника с основанием 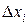и высотой .

.

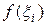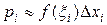Значит, .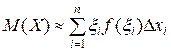

Тогда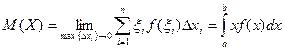

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [ a, b ] называют

.

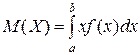Если возможные значения принадлежат всей числовой оси 0 х, то

.

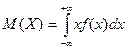Замечание. Предполагается, что несобственный интеграл 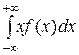сходится абсолютно.