1. Плотность распределения – неотрицательная функция 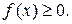
Док-во. Функция распределения F(x) – неубывающая функция, следовательно, ее производная f(x) = F’(x) – неотрицательная функция.
2. Несобственный интеграл от плотности распределения в пределах от -¥ до +¥ равен 1.
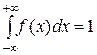 .
.
Док-во. 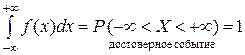 .
.
Частный случай. Если все возможные значения непрерывной случайной величины Х принадлежат интервалу (a, b), то
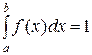 .
.
Геометрическая интерпретация свойств плотности распределения.
1. 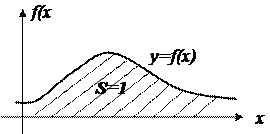 Вся кривая распределения f(x) лежит не ниже оси абсцисс.
Вся кривая распределения f(x) лежит не ниже оси абсцисс.
2. Полная площадь, ограниченная кривой распределения f(x) и осью абсцисс, равна 1.
Механическая интерпретация.
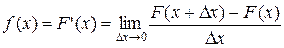 .
.
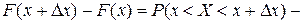 вероятность попадания Х на участок
вероятность попадания Х на участок 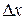 , интерпретируется как масса, приходящая на участок
, интерпретируется как масса, приходящая на участок 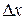 .
.
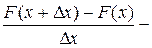 средняя плотность на участке
средняя плотность на участке 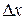 .
.
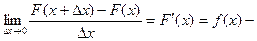 плотность массы в точке
плотность массы в точке 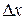 .
.
Пример. Дана функция распределения непрерывной случайной величины Х.
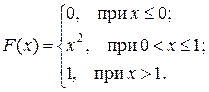
а) найти плотность распределения f(x);
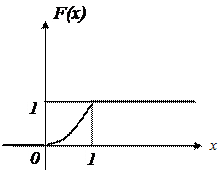
б) графики F(x) и f(x);
в) найти вероятность попадания Х в (0,25; 0,5); (0,5; 0,2).
Решение.
а) 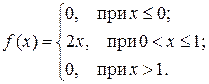
 | |||
 | |||
б)
в) 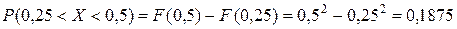 (1-й способ)
(1-й способ)
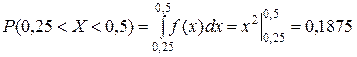 (2-й способ).
(2-й способ).
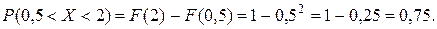
 2015-07-14
2015-07-14 1205
1205
