Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b) равна определенному интегралу от плотности распределения, взятому в пределах от a до b
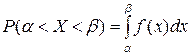 .
.
Док-во. Воспользуемся формулой из §18:
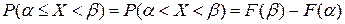 .
.
По формуле Ньютона-Лейбница:
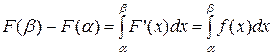 .
.
Отсюда: 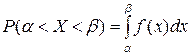 , что и требовалось доказать.
, что и требовалось доказать.
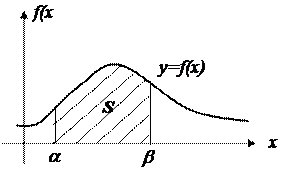 Геометрически. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b) равна площади криволинейной трапеции, ограниченной кривой f(x), осью 0х, прямыми x=a, x= b.
Геометрически. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b) равна площади криволинейной трапеции, ограниченной кривой f(x), осью 0х, прямыми x=a, x= b.
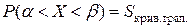 .
.
Нахождение функции распределения по известной плотности распределения
Дано: f(x) – плотность распределения.
Найти: F(x) – функцию распределения.
По определению: 
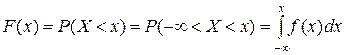 .
.
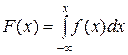 .
.
 2015-07-14
2015-07-14 5397
5397








