Опр. Начальным моментом k -го порядка случайной величины X называют математическое ожидание величины Xk.
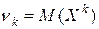
Для дискретной случайной величины: 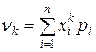
Для непрерывной случайной величины: 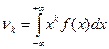
Частные случаи
1. 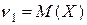 – начальный момент 1-го порядка это математическое ожидание.
– начальный момент 1-го порядка это математическое ожидание.
2. 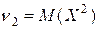
Опр. Центрированной случайной величиной, соответствующей величине X, называется отклонение случайной величины X от ее математического ожидания.
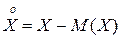
Опр. Центральным моментом k-го порядка случайной величины X называется математическое ожидание k -той степени, соответствующей центрированной случайной величине.
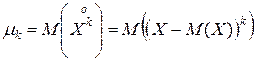
Для дискретной случайной величины: 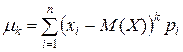
Для непрерывной случайной величины: 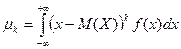
Частные случаи
1. 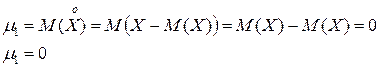
2. 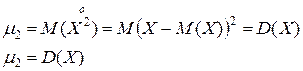
Центральный момент 2-го порядка это дисперсия
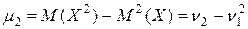 *
*
3. Центральный момент 3-го порядка 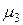 служит для характеристики асимметрии (или «скошенности») распределения. Если распределение симметрично относительно математического ожидания, то
служит для характеристики асимметрии (или «скошенности») распределения. Если распределение симметрично относительно математического ожидания, то 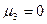 (как и все моменты нечетного порядка), если несимметрично, то
(как и все моменты нечетного порядка), если несимметрично, то 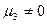
|

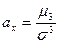 – коэффициент асимметрии
– коэффициент асимметрии
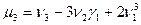
4. Центральный момент 4-го порядка 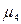 служит для характеристики «крутости» (островершинности или плосковершинности) распределения
служит для характеристики «крутости» (островершинности или плосковершинности) распределения
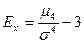 – эксцесс.
– эксцесс.
Соотношения, связывающие центральные и начальные моменты
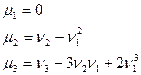
 2015-07-14
2015-07-14 524
524








