Теорема Чебышева

Пусть имеется последовательность случайных величин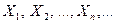

Опр. Говорят, что последовательность случайных величин X_n сходится по вероятности к неслучайной величине a, если при сколь угодно малом положительном числе 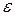вероятность неравенства 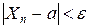с увеличением n неограниченно приближается к единице.

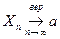или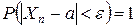

Различия между сходимостью в смысле обычного математического анализа (1) и сходимостью по вероятности (2) в следующем:

(1)

(2) для отдельных значений n неравенство может не выполняться.

Закон больших чисел устанавливает условия сходимости по вероятности (тех или иных) случайных величин к определенным постоянным.

Теорема Чебышева (одна из важных форм закона больших чисел)

Если 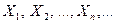попарно независимые случайные величины, причем их дисперсии равномерно ограничены (не превышают постоянного числа c), то

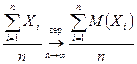или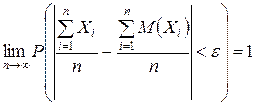

Док-во:

Обозначим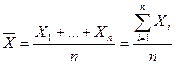

Применим к случайной величине 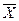неравенство Чебышева

*

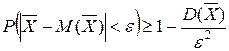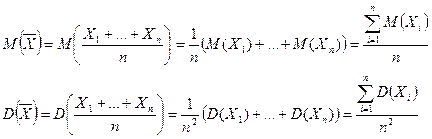
По условию 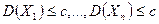значит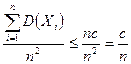

Подставим в (*)

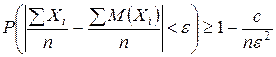
Перейдем к 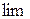при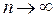

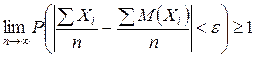
Т.к. вероятность не может быть >1, то 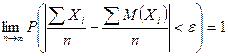, что и требовалось доказать.