При построении и исследовании математических моделей необходимо учитывать не только основные свойства элементарных функций, рассматриваемые ранее. Одной из важных характеристик функции является скорость ее изменения. Определить скорость изменения функции можно с помощью касательных к графику функции. Чем ближе угол наклона касательной к оси Ох к 90°, тем выше скорость изменения функции.
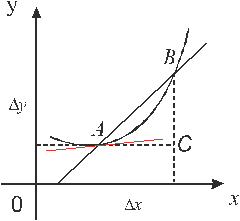 |
Через точки
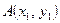 и
и 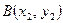 проведем к графику данной функции секущую. Обозначим
проведем к графику данной функции секущую. Обозначим 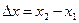 ,
, 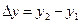
Определим угол наклона секущей относительно оси Ох: 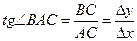
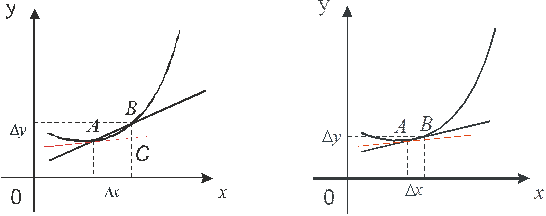
Устремим 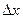 к нулю. Тогда точка В устремиться к точке А, а секущая АВ будет стремиться к касательной, проходящей через точку А.
к нулю. Тогда точка В устремиться к точке А, а секущая АВ будет стремиться к касательной, проходящей через точку А.
Т.е. при 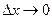
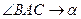 , где
, где 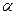 – угол наклона касательной к оси Ох,
– угол наклона касательной к оси Ох, 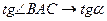 .
.
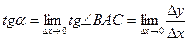
Производной функции 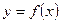 называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует).
называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует).
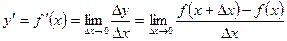 .
.
Если функция в точке 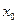 (или в каждой точке промежутка Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (на этом промежутке).
(или в каждой точке промежутка Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (на этом промежутке).
Если функция 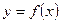 дифференцируема в точке
дифференцируема в точке 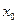 (или в каждой точке промежутка Х), то она в этой точке (или на промежутке) непрерывна. Если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке.
(или в каждой точке промежутка Х), то она в этой точке (или на промежутке) непрерывна. Если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке.
Геометрический смысл производной: производная 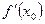 есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой
есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой 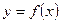 в точке
в точке 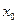 , т.е.
, т.е. 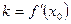 .
.
Тогда уравнение касательной к кривой 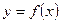 в точке
в точке 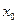 примет вид
примет вид
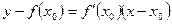 .
.
 2015-07-14
2015-07-14 402
402








