Непрерывность функции

Функция 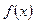называется непрерывной в точке 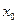, если она удовлетворяет следующим условиям: 1) определена в точке 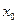(т.е. существует 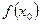); 2) имеет конечный предел функции при 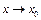; 3) этот предел равен значению функции в точке 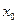, т.е. .

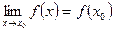Функция 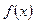называется непрерывной в точке 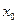, если она определена в точке 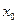и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: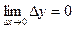

Свойства функций, непрерывных в точке:

Если функци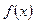и и 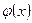непрерывны в точке 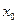, то их сумма 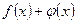, произведение 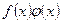и частное 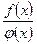(при условии, что 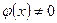) являются функциями, непрерывными в точке .

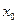Если функция 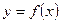непрерывна в точке 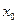и 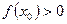, то существует такая окрестность точки 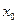, в которой .

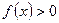Если функция 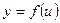непрерывна в точке 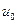, а функция 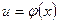непрерывна в точке 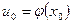, то сложная функция 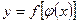непрерывна в точке .

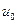Функция 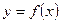называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.

Можно доказать, что все элементарные функции непрерывны в области их определения.