2015-07-14
473
Асимптотой графика функции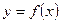 
называется прямая, обладающая следующим свойством. Расстояние от точки 
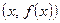до этой прямой стремиться к нулю при неограниченном удалении точки графика от начала координат.
Теорема 1. Пусть функция 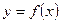определена в некоторой окрестности точки 
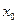(исключая, быть может, саму эту точку), и хотя бы один из пределов функции при 
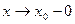(слева) или при 
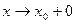(справа) равен бесконечности, т.е. 
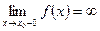или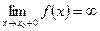 
. Тогда прямая 
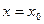является вертикальной асимптотой графика функции .
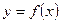Вертикальные асимптоты 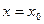следует искать в точках разрыва функции 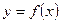или на концах ее области определения 
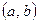, если а и b – конечные числа.
Теорема 2. Пусть функция 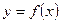определена при достаточно больших х и существует конечный предел функции 
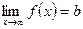. Тогда прямая 
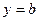есть горизонтальная асимптота графика функции .
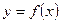Если конечен только один из пределов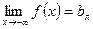 
или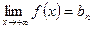 
, то функция имеет лишь левостороннюю 
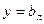или правостороннюю 
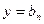асимптоту.
Теорема 3. Если функция 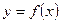определена при достаточно больших х, и существуют конечные пределы 
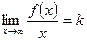и 
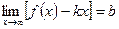. Тогда прямая 
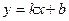является наклонной асимптотой графика функции.
|
|
|
