1. Найти производную данной функции.
2. Найти критические точки функции.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии точек экстремума.
4. Найти экстремумы функции.
Второе достаточное условие экстремума. Если первая производная 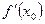 дважды дифференцируемой функции равна нулю в некоторой точке
дважды дифференцируемой функции равна нулю в некоторой точке 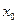 , а вторая производная в этой точке
, а вторая производная в этой точке 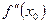 положительна (отрицательна), то
положительна (отрицательна), то 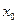 есть точка минимума (максимума) функции
есть точка минимума (максимума) функции 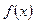 .
.
 2015-07-14
2015-07-14 1832
1832
