Производная функции в точке

Рассмотрим функцию 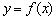(синяя линия), которая определена и непрерывна на некотором интервале, произвольную точку 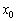, принадлежащую данному интервалу, и соответствующее значение :

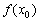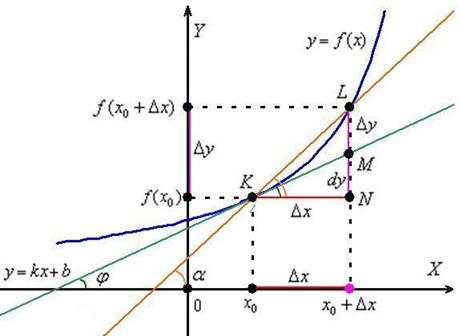
Зададим аргументу функции приращение 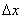(красный отрезок) в точке 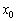. Обратите внимание, что 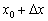– это тоже вполне определённая точка нашего интервала (на всякий случай отметил её малиновым цветом). И в этой точке существует своё значение функции .

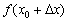Приращение аргумента 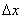повлекло за собой приращение функции:
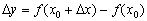(малиновый отрезок)

В данном случае 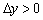, поскольку в качестве примера выбран промежуток, на котором функция возрастает.

Давайте сразу возьмём на заметку, что нарисовалась в результате проделанных действий. Ну, конечно же, в глаза бросается секущая 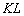(коричневая прямая) и прямоугольный треугольник .

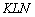Угол наклона секущей к оси 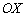я обозначил через 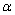и отметил его коричневой дугой в двух местах. Такое внимание к данному углу не случайно – он однозначно определяется приращениями 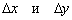. Рассмотрим прямоугольный треугольник 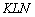и угол 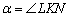. Согласно школьному определению, тангенс угла равен отношению противолежащего катета к прилежащему катету: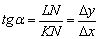

Определение: производной функции в точке 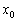называется предел отношения приращения функции 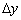к вызвавшему его приращению аргумента 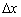в этой точке при 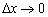. Или коротко:

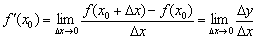
Если данный предел конечен, то функция 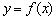является дифференцируемой в точке 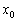. А то, что в львиной доле случаев предел 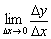существует и конечен, скептики убедятся в самом ближайшем будущем.

ВАЖНЫЙ МОМЕНТ состоит в том, что приращение аргумента стремится к нулю, но нуля не достигает, иными словами, величина 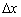бесконечно малА, но не равна нулю!