2015-07-14
548
Пожалуйста, возьмите в руки обычную линейку и совместите её ребро с прямой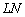 
.
Да-да – приложите прямо к экрану монитора, не комплексуйте =) Вместо линейки можно использовать тетрадку, лист бумаги или даже руку.
Теперь, согласно определению производной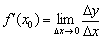 
, медленно двигаем линейку влево к точке 
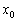, уменьшая тем самым приращение 
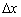. При этом приращение функции 
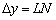тоже уменьшается: точка 
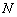будет бесконечно близко приближаться к точке 
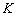по горизонтали (красному отрезку), и точка 
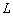– бесконечно близко приближаться к той же точке 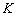, но уже по графику функции 
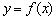(синей линии).
В результате секущая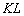
стремится занять положение касательной 
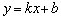к графику функции 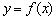в точке 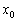. Искомая касательная изображена зелёным цветом.
Таким образом, мы получили строгое определение касательной к графику функции:
Касательная к графику функции в точке – это предельное положение секущей в данной точке.
Вот что матан животворящий делает =)
Развиваем мысль дальше. Вспомним полученную ранее формулу тангенса угла наклона секущей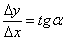 
и осуществим в обеих её частях так называемый предельный переход.
В свете рассматриваемых событий (бесконечного уменьшения 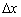и нахождения предела 
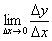) угол наклона 
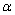секущей 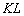стремится к углу наклона
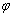касательной 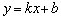(последний дважды отмечен зелёными дугами). Аналогичное утверждение справедливо и для тангенсов данных углов: 
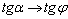. В итоге:
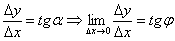
Вывод: производная функции в точке 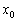численно равна тангенсу угла наклона касательной к графику функции в данной точке: 
.
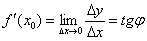А тангенс угла наклона касательной – это в точности её угловой коэффициент:
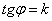
В курсе аналитической геометрии выведена формула, по которой можно составить уравнение прямой с угловым коэффициентом:
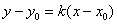
Учитывая полученное равенство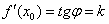 
, перепишем уравнение в виде 
.
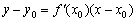Данной формулой мы уже активно пользовались, когда находили уравнение касательной, и сейчас стало ясно, откуда она взялась.
