Существование производной в точке и непрерывность функции

По определению: 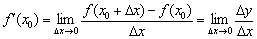, следовательно, существование производной в точке 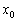тесно связано с существованием предела 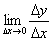в данной точке.

Я изо всех сил пытался отсрочить этот момент, чтобы не путать посетителей сайта, но рассказать всё равно придётся…. В определении производной ВАЖНЕЙШИМ является тот факт, что приращение аргумента 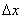задаётся и в другую сторону. Возьмите карандаш и листок бумаги (не ленимся – так будет в 10 раз понятнее!!!!). Изобразите координатные оси, примерно такой же график функции 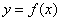и точки .

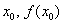Отложите на чертеже небольшой отрезок 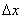слева от точки 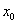. При этом точка 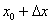расположится левее точки 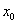, а точка 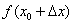– ниже точки 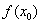. Теперь проведите секущую графика функции 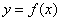и начните мысленно уменьшать приращение 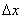вправо к точке 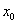. В результате данная секущая будет стремиться занять положение той же самой «зелёной» касательной!

Примечание: приращение с левой стороны осуществляется «против оси абсцисс» и поэтому отрицательно: 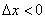. Заметьте, что всё остаётся корректным, так, в нашем случае соответвующие приращение 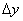тоже меньше нуля, и по этой причине левосторонний предел таки будет положительным 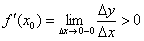, корректно показывая (как и его правосторонний коллега) рост функции в точке 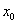. Односторонние пределы конечны и совпадают, что говорит о существовании общего предела, производной и единой касательной.

Таким образом, существование производной в точке геометрически очень удобно ассоциировать с существованием ОБЩЕЙ КАСАТЕЛЬНОЙ в данной точке.

Очевидно, что функция не дифференцируема в точках разрыва. Во-первых, она может быть не определена в такой точке, следовательно, приращение 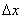задать невозможно (на нет и суда нет). А во-вторых, практически всегда попросту не существует общего предела 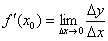(по причине различных «нехорошестей» с односторонними пределами). Читатели, насмотревшиеся графиков разрывных функций (это намёк;-) =)), легко представят проблему с общей касательной.

Вывод: из дифференцируемости функции в точке 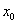необходимо (обязательно) следует её непрерывность в данной точке.

Однако обратное утверждение в общем случае неверно, то есть из непрерывности функции дифференцируемость следует далеко не всегда! Классический пример, функция 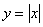в точке 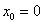(чертёж есть в Примере 24 урока о геометрических преобразованиях графика ). Если рассмотреть приращение 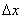справа, то правосторонний предел будет равен 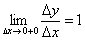, и, соответственно, получаем касательную 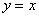, совпадающую с правой частью графика 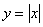. Если же придать приращение аргументу 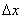влево, получается совсем другой результат: 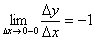и другая касательная 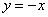, которая совпадает с левой частью графика 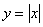. Печалька. Ни общего предела, ни общей касательной. Таким образом, функция 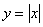хоть и непрерывна в точке 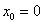, но не дифференцируема в ней! Подробное аналитическое доказательство проводится по шаблону Примера 11 статьи Производная по определению. Ещё один типичный образец есть в Примере 6 урока Непрерывность функции, где кусочно-заданная функция непрерывна на . Однако не всё так безоблачно – она не дифференцируема в точках «стыка» графика.

В заключение параграфа немного об особых случаях.

Когда предел 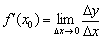равен «плюс» или «минус бесконечности», то производная тоже существует и касательная к графику функции будет параллельная оси 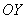. Например, касательной к графику функции 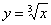(см. чертёж Примера 6 урока Методы решения определённых интегралов ) в точке 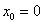является сама ось ординат. Более того, если односторонние пределы бесконечны и различны по знаку, то единая касательная и производная всё равно могут существовать! Пожалуйста: квадратный корень из модуля «икс» в той же точке .

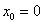За более детальной и подробной информацией по сабжу можно обратиться, например, к первому тому Фихтенгольца. НедУрно издание 1962 года, закачивается без проблем.

Раз пошла такая пьянка...: