Понятие производной функции

До сих пор речь шла о производной и дифференциале в единственной «подопытной» точке 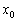. Но ведь в качестве 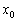можно взять ЛЮБУЮ ТОЧКУ 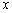рассматриваемого интервала!
Из этих соображений в равенстве 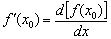проведём замену 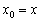и получим 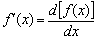. А это ни что иное, как обозначение производной 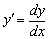, о котором я упомянул на первом же уроке по технике дифференцирования. Символ 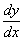используется двояко – и как цельный символ производной, и как частное дифференциалов. Вторая интерпретация активно эксплуатируется в ходе решения дифференциальных уравнений.

Естественно, и в самом определении производной в точке 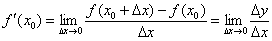заменим 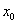на :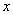

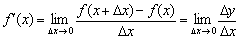
К чему мы пришли? А пришли мы к тому, что для функции 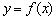по закону 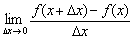ставится в соответствие другая функция 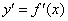, которая называется производной функцией (или просто производной).

Производная 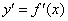характеризует скорость изменения функции 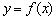. Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку 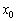области определения функции 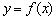. Пусть функция дифференцируема в данной точке. Тогда:

1) Если 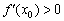, то функция 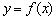возрастает в точке 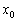. И, очевидно, существует интервал (пусть даже очень малый), содержащий точку 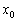, на котором функция 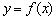растёт, и её график идёт «снизу вверх».

2) Если 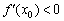, то функция 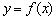убывает в точке 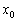. И существует интервал, содержащий точку 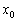, на котором функция 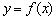убывает (график идёт «сверху вниз»).

3) Если 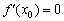, то бесконечно близко около точки 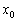функция 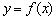сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции, в частности в точках минимума и максимума.

Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию 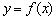, мы «выделяем» скорость её изменения в виде производной функции 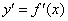. А что, кстати, понимается под словом «производная»? Функция 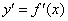произошла от функции .

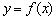Термины весьма удачно истолковывает механический смысл производной:
Рассмотрим закон изменения координаты тела 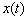, зависящий от времени 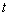, и функцию скорости движения данного тела 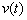. Функция 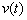характеризует скорость изменения координаты тела, поэтому является первой производной функции 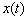по времени: 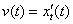. Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».

Ускорение тела 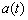– это скорость изменения скорости, поэтому: 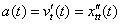. Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».

Откуда взялись правила дифференцирования и таблица производных? Невероятно, но все они появились благодаря единственной формуле: 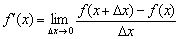. И как это происходит, мы начнём разбирать прямо сейчас.

Действительно, пора переходить к практическим примерам. Ну а это был, пожалуй, первый обстоятельный теоретический материал, который я опубликовал на сайте – вполне можете взять для реферата или курсовика. Только аккуратнее, здесь есть зашифрованное послание для вашего преподавателя =)

Пример 1

Используя определение производной, доказать, что производная константы равна нулю.

Функция-константа имеет вид 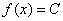, и графически – это семейство прямых, параллельных оси абсцисс. Наверное, многие уже догадались, почему .
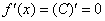Изобразим, например, график функции :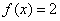

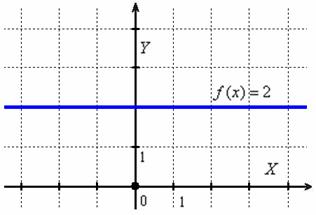
Это «ровная дорога», то есть функция и не возрастает и не убывает в каждой точке. Ни вверх и не вниз.

Покажем аналитически, что производная функции-константы равна нулю. Рассмотрим произвольное значение 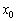, в котором, понятно, 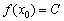. Придадим аргументу приращение: 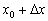. Функция всё время постоянна, поэтому 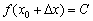и приращение функции: 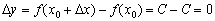. По определению производной в точке:

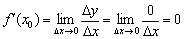
Заметьте, тут нет неопределённости: ноль, делённый на бесконечно малое число 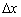, равен нулю. Пытливые читатели могут взять в руки калькулятор и убедиться в этом.

Поскольку в качестве точки 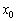можно взять любое «икс», то проведём замену 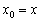и получим: .

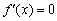Пример 2

Найти производную функции 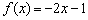по определению.

Рассмотрим произвольное значение 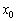, в котором .

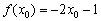Зададим аргументу приращение 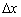и вычислим соответствующее значение функции: 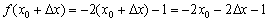(обычная алгебра – в функцию 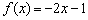вместо «икса» подставили 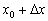и раскрыли скобки).

Вычислим приращение функции:

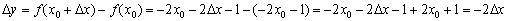
По определению производной в точке:

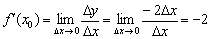
Поскольку в качестве 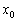можно взять любое значение 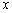, то .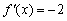

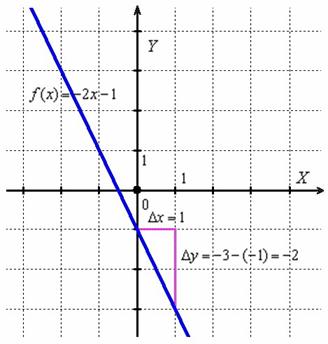
О чём нам говорит найденная производная? Во-первых, для любого «икс» она отрицательна, а значит, функция 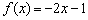убывает на всей области определения. И, во-вторых, это убывание постоянно, то есть «наклон горки везде одинаков» – в какой бы точке мы не находились, предельное отношение 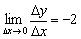будет неизменным:

Здесь и далее я предполагаю, что читатель умеет находить, как минимум, простые производные, пользуясь правилами дифференцирования и таблицей. Давайте найдём производную «быстрым» способом: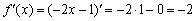

Теперь вам должно быть понятно происхождение и весь неформальный смысл полученного результата.

Используя этот же алгоритм, можно решить задачу в общем виде и доказать, что производная линейной функции 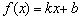равна её угловому коэффициенту:
.

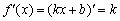В начале статьи Уравнение прямой на плоскости я проанализировал расположение прямой в зависимости от углового коэффициента. И сейчас получено объяснение данных фактов с точки зрения математического анализа. Действительно, рассмотрим две линейные функции 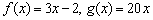и найдём их производные:

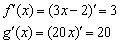
Обе производные положительны, а значит, функции возрастают на всей области определения (графики идут «снизу вверх»). Кроме того, не забываем, что производная – это мера скорости изменения функции. Поскольку 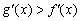, то функция 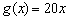растёт быстрее (причём, значительно) функции 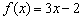, и, соответственно, график 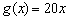намного более крут.

Факт тривиален, но озвучу: касательная к графику линейной функции в каждой точке совпадает с самим графиком данной линейной функции.

Заключительная демонстрационная задача, думаю, развеет все оставшиеся непонятки:

Пример 3

Найти производную функции 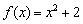по определению.

Рассмотрим произвольную точку 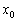и соответствующее значение 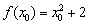. Зададим приращение 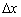и вычислим значение функции во второй точке:

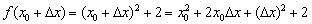
Найдём приращение функции:

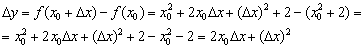
По определению производной в точке:

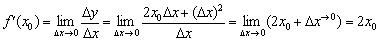
Поскольку в качестве 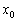можно рассмотреть любую точку 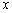области определения функции 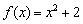, то проведём замену 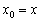и получим .

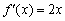Проверим результат «лёгким» способом: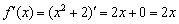

Вообще говоря, исходная функция 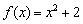и её производная 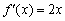– это две совершенно разные функции, однако между ними существует чёткая и прозрачная связь:

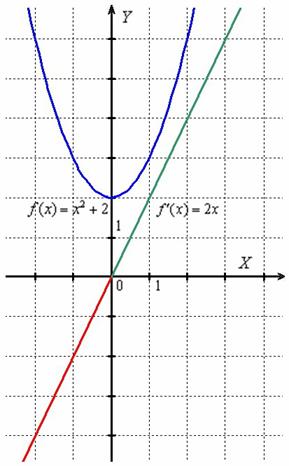
На интервале 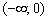производная отрицательна: 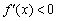(красная линия), что говорит об убывании функции 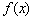на данном интервале. Грубо говоря, график идёт сверху вниз.

А на интервале 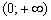производная положительна: 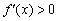(зелёная линия), значит, функция 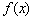растёт на этом интервале, а её график идёт снизу вверх.

При 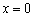производная равна нулю: 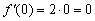. Найденное значение показывает, что скорость изменения функции 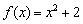в точке 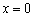равна нулю (функция не растёт в ней и не убывает). В данном случае здесь минимум функции.

Всё это можно утверждать даже не зная, что такое парабола и как выглядит график функции !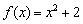

И ещё раз заостряю внимание, что значение производной в точке выражает собой некоторую меру скорости изменения функции в данной точке. Найдём несколько значений производной:

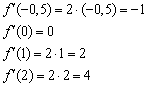
Таким образом, в точке 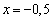функция 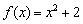убывает, в точке 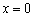сохраняет скорость постоянной, а в точках 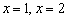– растёт. Причём 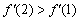, поэтому можно сказать (опять даже не зная чертежа!), что в окрестности точки 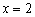график функции 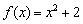идёт вверх круче, чем вблизи точки .

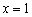Закрепим геометрический смысл: производная в точке численно равна тангенсу угла наклона касательной к графику функции в данной точке. Не поленюсь, применю формулу 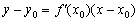четыре раза:

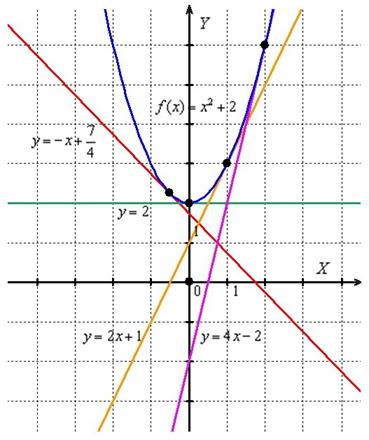
Вот так вот изящно производная характеризует свою функцию.

Я долго сомневался, в какой раздел отнести данную статью, и всё-таки решил поставить её в месте логического появления – раздел «Функции и графики». К дальнейшему изучению рекомендую урок об экстремумах функции. А производная по определению, которую мы уже начали рассматривать и которая является отдельной самостоятельной задачей, пусть будет в «техническом» разделе о дифференцировании. И смех, и грех, но для применения формулы 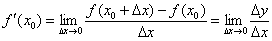опять же совсем не обязательно понимать, что это производная =)

Желаю успехов!

Автор: Емелин Александр