Дифференциалом функции 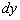 в точке
в точке 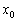 называют главную линейную часть приращения функции
называют главную линейную часть приращения функции 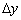 (строго говоря, его следовало обозначить
(строго говоря, его следовало обозначить 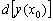 или
или 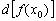 ). На чертеже дифференциал
). На чертеже дифференциал 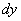 в точке
в точке 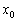 равен длине отрезка
равен длине отрезка 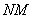 .
.
Давайте снова возьмём в руки линейку и приложим её ребром к монитору на прямую 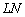 . Двигая линейку влево к точке
. Двигая линейку влево к точке 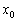 , уменьшаем приращение
, уменьшаем приращение 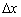 . Впрочем, и сам выполню несколько засечек:
. Впрочем, и сам выполню несколько засечек:
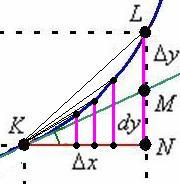
По рисунку хорошо видно, что с уменьшением 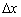 (а значит, и уменьшением
(а значит, и уменьшением 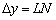 – малиновых линий) отрезок
– малиновых линий) отрезок 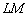 занимает всё меньшую и меньшую часть приращения, а наш дифференциал
занимает всё меньшую и меньшую часть приращения, а наш дифференциал 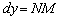 – всю бОльшую и бОльшую его часть, именно поэтому его и называют главной частью приращения
– всю бОльшую и бОльшую его часть, именно поэтому его и называют главной частью приращения 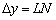 . Настолько главной, что при бесконечно малом
. Настолько главной, что при бесконечно малом 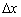 дифференциал стремится к полному приращению функции:
дифференциал стремится к полному приращению функции: 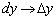 (соответственно отрезок
(соответственно отрезок 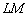 будет бесконечно малым).
будет бесконечно малым).
Нетрудно вывести формулу для приближенных вычислений с помощью дифференциала. Рассмотрим прямоугольный треугольник 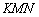 и тангенс угла наклона касательной
и тангенс угла наклона касательной 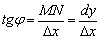 . Обозначив дифференциал в рассматриваемой точке
. Обозначив дифференциал в рассматриваемой точке 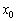 корректнее через
корректнее через 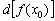 , и учитывая, что
, и учитывая, что 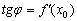 , получаем:
, получаем:
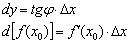
То есть идея формулы приближенных вычислений 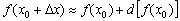 состоит в том, чтобы точное значение
состоит в том, чтобы точное значение 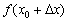 функции (смотрим на ось ординат основного чертёжа) заменить суммой
функции (смотрим на ось ординат основного чертёжа) заменить суммой 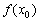 и отрезка
и отрезка  . К слову, отрезок
. К слову, отрезок 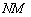 на главном чертеже существенно «не достаёт» до полного приращения
на главном чертеже существенно «не достаёт» до полного приращения 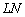 , и это не случайность. В демонстрационной иллюстрации я выбрал большое значении
, и это не случайность. В демонстрационной иллюстрации я выбрал большое значении 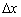 , чтобы всё было видно. На практике же, чем приращение
, чтобы всё было видно. На практике же, чем приращение 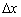 меньше – тем дифференциал лучше «дотянется» до полного приращения функции (см. маленький рисунок), и тем точнее сработает формула
меньше – тем дифференциал лучше «дотянется» до полного приращения функции (см. маленький рисунок), и тем точнее сработает формула 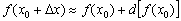 .
.
Провернём ещё один неожиданный фокус с полученным равенством 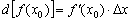 . Предельно малое значение
. Предельно малое значение 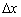 часто обозначают через
часто обозначают через 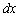 , поэтому формула принимает вид
, поэтому формула принимает вид 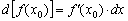 . Скинем
. Скинем 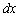 в знаменатель противоположной части:
в знаменатель противоположной части:
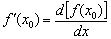
 2015-07-14
2015-07-14 652
652








