Задание 1. Вычислить криволинейные интегралы I-го рода:
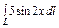 , где L – дуга кривой , где L – дуга кривой 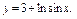 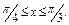 | 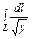 где L – дуга циклоиды где L – дуга циклоиды 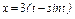 , , 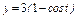 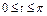 | 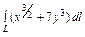 где L – дуга параболы где L – дуга параболы 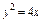 от точки от точки 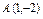 до точки до точки 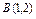 . . | |||
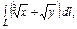 где L – отрезок прямой, соединяющей точки где L – отрезок прямой, соединяющей точки 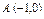 . и . и 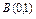 | 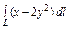 где L – контур треугольника с вершинами где L – контур треугольника с вершинами 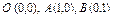 | 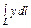 где L – дуга параболы где L – дуга параболы 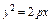 , отсечённая парабола , отсечённая парабола 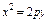 | |||
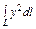 где L – арка циклоиды где L – арка циклоиды 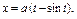 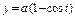 , , 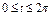 | 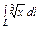 , где L – дуга астроиды , где L – дуга астроиды 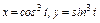 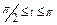 | 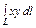 где L – дуга гиперболы где L – дуга гиперболы 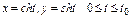 | |||
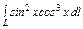 где L – дуга кривой где L – дуга кривой 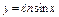 , , 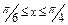 | 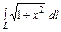 где L – дуга кривой где L – дуга кривой 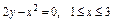 | 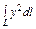 , где L – дуга кривой , где L – дуга кривой 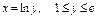 | |||
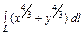 где L – дуга астроиды где L – дуга астроиды 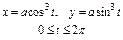 | 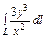 где L – дуга кривой где L – дуга кривой 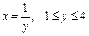 | 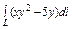 где L – дуга параболы где L – дуга параболы 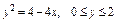 | |||
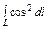 где L – дуга кривой где L – дуга кривой 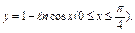 | 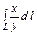 где L – дуга параболы где L – дуга параболы 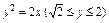 | 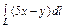 где L – контур треугольника с вершинами где L – контур треугольника с вершинами 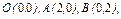 | |||
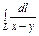 где L – отрезок прямой, соединяющей точки где L – отрезок прямой, соединяющей точки 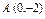 и и 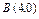 . . | 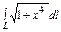 где L – дуга кривой где L – дуга кривой 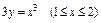 | 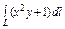 где L – отрезок прямой, соединяющей точки где L – отрезок прямой, соединяющей точки 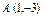 и и 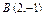 | |||
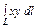 , где L – контур квадрата , где L – контур квадрата 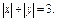 | 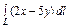 где L –контур квадрата где L –контур квадрата 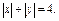 | 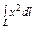 где L – верхняя половина окружности где L – верхняя половина окружности 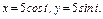 | |||
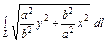 где L – дуга эллипса где L – дуга эллипса 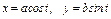 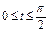 | 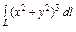 где L – дуга окружности где L – дуга окружности 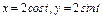 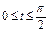 | 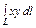 где L – четверть эллипса где L – четверть эллипса 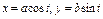 лежащая в первом квадранте. лежащая в первом квадранте. | |||
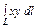 где L – контур прямоугольника с вершинами где L – контур прямоугольника с вершинами 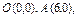 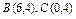 . . | 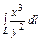 где L – дуга кривой где L – дуга кривой 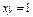 между точками между точками 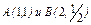 | 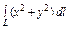 где L – дуга развёртки окружности где L – дуга развёртки окружности 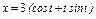 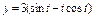 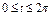 |
Задание 2. Вычислить криволинейные интегралы I-го рода.
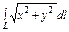 где L – верхняя половина кардиоиды где L – верхняя половина кардиоиды 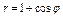 | 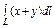 где L – правый лепесток лемнискаты где L – правый лепесток лемнискаты 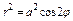 | 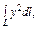 где L – верхняя полуокружность где L – верхняя полуокружность 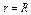 | |||
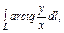 где L – часть спирали Архимеда где L – часть спирали Архимеда 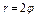 , заключённая внутри круга радиуса R с центром в начале координат (в полюсе). , заключённая внутри круга радиуса R с центром в начале координат (в полюсе). | 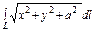 , где L - дуга спирали Архимеда , где L - дуга спирали Архимеда 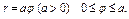 | 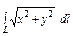 , где L – дуга лемнискаты , где L – дуга лемнискаты 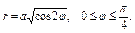 | |||
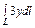 , где L – дуга кардиоиды , где L – дуга кардиоиды 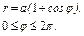 | 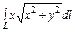 , где L – граница кругового сектора , где L – граница кругового сектора 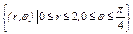 | 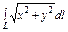 , где L – окружность , где L – окружность 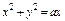 | |||
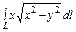 , где L – дуга лемнискаты , где L – дуга лемнискаты 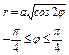 | 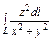 , где L – первый виток линии , где L – первый виток линии 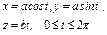 | 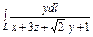 , где L – дуга линии , где L – дуга линии 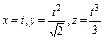 от точки от точки 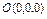 до точки до точки 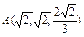 | |||
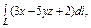 где L – отрезок прямой, соединяющей точки где L – отрезок прямой, соединяющей точки 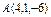 и и 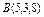 | 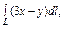 где L – дуга окружности где L – дуга окружности 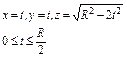 | 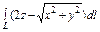 где L – первый виток конической винтовой линии где L – первый виток конической винтовой линии 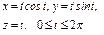 | |||
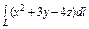 где L – отрезок прямой, соединяющей точки где L – отрезок прямой, соединяющей точки 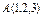 и и 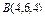 | 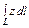 где L – первый виток конической винтовой линии где L – первый виток конической винтовой линии 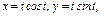 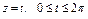 | 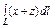 где L – дуга кривой где L – дуга кривой 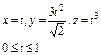 | |||
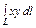 где L – дуга винтовой линии где L – дуга винтовой линии 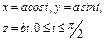 | 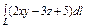 где L – отрезок прямой, соединяющей точки где L – отрезок прямой, соединяющей точки 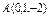 и и 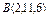 | 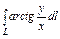 , где L – часть дуги спирали Архимеда , где L – часть дуги спирали Архимеда 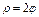 , заключенная внутри круга радиусом R с центром в полюсе. , заключенная внутри круга радиусом R с центром в полюсе. | |||
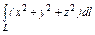 ,где L – дуга кривой ,где L – дуга кривой 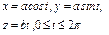 | 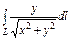 , где L - дуга кардиоиды , где L - дуга кардиоиды 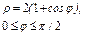 | 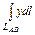 , где L - дуга астроиды , где L - дуга астроиды 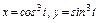 между точками между точками 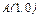 и и 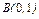 . . | |||
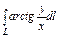 , где L - дуга кривой , где L - дуга кривой 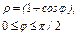 | 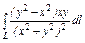 , где L - дуга кривой , где L - дуга кривой 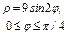 | 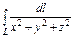 ,где L – первый виток винтовой линии ,где L – первый виток винтовой линии 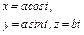 | |||
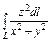 ,где L – первый виток винтовой линии ,где L – первый виток винтовой линии 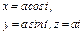 | 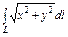 ,где L – развертка окружности ,где L – развертка окружности 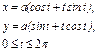 | 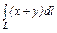 , где L – дуга лемнискаты Бернулли , где L – дуга лемнискаты Бернулли 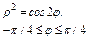 |
Задание 3. Вычислить криволинейные интегралы 2-го рода:
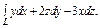 где L – виток винтовой линии где L – виток винтовой линии 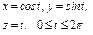 | 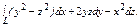 где L – дуга кривой где L – дуга кривой 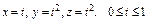 | 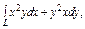 где L – дуга кривой где L – дуга кривой 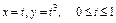 | |||
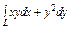 , где L – дуга кривой , где L – дуга кривой 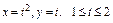 | 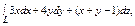 где L – отрезок прямой от точки где L – отрезок прямой от точки 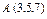 до точки до точки 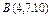 | 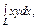 где L – дуга эллипса где L – дуга эллипса 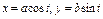 от точки от точки 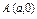 до точки до точки 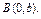 | |||
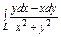 , где L – окружность , где L – окружность 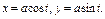 пробегаемая в положительном направлении. пробегаемая в положительном направлении. | 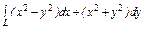 , где L – эллипс , где L – эллипс 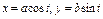 , пробегаемый в положительном направлении , пробегаемый в положительном направлении | 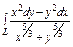 , где L – четверть астроиды , где L – четверть астроиды 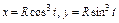 от точки от точки 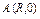 до точки до точки 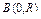 | |||
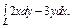 где L – контур треугольника с вершинами где L – контур треугольника с вершинами 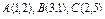 , пробегаемый в положительном направлении. , пробегаемый в положительном направлении. | 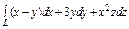 , где L –отрезок прямой от точки , где L –отрезок прямой от точки 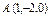 до точки до точки 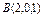 | 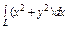 , где L – контур прямоугольника, образованного прямыми , где L – контур прямоугольника, образованного прямыми 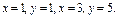 Интегрирование вести в положительном направлении. Интегрирование вести в положительном направлении. | |||
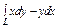 , вдоль кривой , вдоль кривой 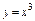 от точки от точки 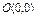 до точки до точки 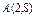 | 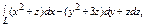 где L - отрезок прямой от точки где L - отрезок прямой от точки 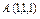 до точки до точки 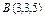 | 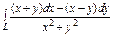 , где L - окружность , где L - окружность 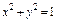 , пробегаемая в положительном направлении. , пробегаемая в положительном направлении. | |||
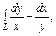 где L – первая четверть окружности, где L – первая четверть окружности, 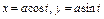 пробегаемая против хода часовой стрелки. пробегаемая против хода часовой стрелки. | 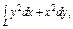 где L – верхняя половина эллипса где L – верхняя половина эллипса 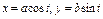 , пробегаемая по ходу часовой стрелки. , пробегаемая по ходу часовой стрелки. | 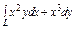 , где L – контур, ограниченный параболами , где L – контур, ограниченный параболами 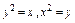 и пробегаемый против хода часовой стрелки. и пробегаемый против хода часовой стрелки. | |||
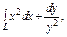 где L – дуга кривой где L – дуга кривой 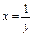 от точки от точки 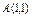 до точки до точки 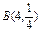 | 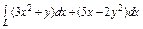 , где L – контур треугольника с вершинами , где L – контур треугольника с вершинами 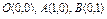 , пробегаемый против хода часовой стрелки. , пробегаемый против хода часовой стрелки. | 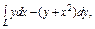 где L – дуга параболы где L – дуга параболы 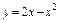 , расположенная над осью OX и пробегаемая против хода часовой стрелки. , расположенная над осью OX и пробегаемая против хода часовой стрелки. | |||
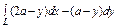 , где L – арка циклоиды , где L – арка циклоиды 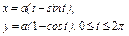 | 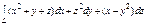 , где L – отрезок прямой от точки , где L – отрезок прямой от точки 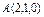 до точки до точки 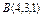 | 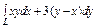 , вдоль линии , вдоль линии 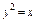 от точки от точки 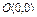 до точки до точки 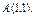 | |||
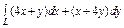 , вдоль линии , вдоль линии 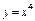 от точки от точки 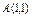 до точки до точки 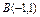 | 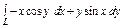 , вдоль прямой , вдоль прямой 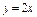 от точки от точки 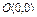 до точки до точки 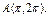 | 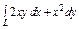 , вдоль линии , вдоль линии 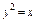 от точки от точки 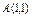 до точки до точки 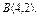 | |||
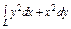 , вдоль прямой , вдоль прямой 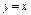 от точки от точки 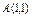 до точки до точки 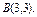 | 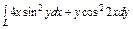 , вдоль прямой , вдоль прямой 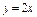 от точки от точки 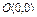 до точки до точки 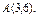 | 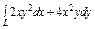 , вдоль параболы , вдоль параболы 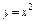 от точки от точки 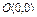 до точки до точки 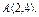 |
Задание 4. Вычислить криволинейные интегралы 2-го рода.
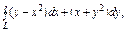 где контур L – ограничивает круговой сектор радиуса R с углом где контур L – ограничивает круговой сектор радиуса R с углом 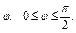 | 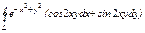 , где L – окружность , где L – окружность 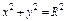 | 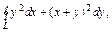 где L – контур треугольника с вершинами где L – контур треугольника с вершинами 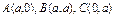 | |||
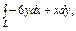 где L – окружность где L – окружность 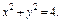 | 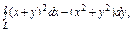 где L – контур треугольника с вершинами где L – контур треугольника с вершинами 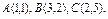 | 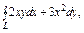 где контур фигуры, ограниченной линиями где контур фигуры, ограниченной линиями 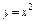 и и 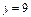 | |||
Вычислить интеграл по замкнутому контуру 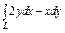 , если , если 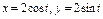 в направлении возрастания параметра в направлении возрастания параметра 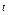 . . | Вычислить интеграл по замкнутому контуру 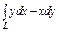 , если , если 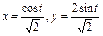 в направлении возрастания параметра в направлении возрастания параметра 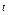 . . | Вычислить интеграл по замкнутому контуру 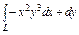 , если , если 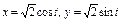 в направлении возрастания параметра в направлении возрастания параметра 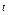 . . | |||
Вычислить интеграл по замкнутому контуру 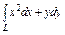 , если , если 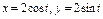 , в направлении возрастания параметра , в направлении возрастания параметра 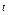 . . | Вычислить интеграл по замкнутому контуру 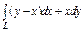 , если , если 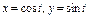 в направлении возрастания параметра в направлении возрастания параметра 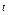 . . | Вычислить интеграл по замкнутому контуру 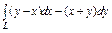 , если , если 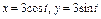 в направлении возрастания параметра в направлении возрастания параметра 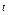 . . | |||
Вычислить интеграл по замкнутому контуру 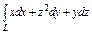 , если , если 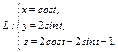 в направлении возрастания параметра в направлении возрастания параметра 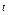 . . | Вычислить интеграл по замкнутому контуру 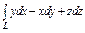 , если , если 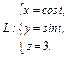 в направлении возрастания параметра в направлении возрастания параметра 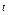 . . | Вычислить интеграл по замкнутому контуру 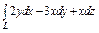 , если , если 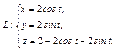 в направлении возрастания параметра в направлении возрастания параметра 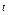 . . | |||
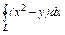 , где L – контур прямоугольника, образованного прямыми , где L – контур прямоугольника, образованного прямыми 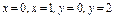 при положительном направлении обхода контура при положительном направлении обхода контура | Вычислить интеграл по замкнутому контуру 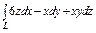 , если , если 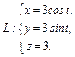 в направлении возрастания параметра в направлении возрастания параметра 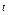 . . | Вычислить интеграл по замкнутому контуру 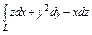 , если , если 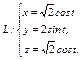 в направлении возрастания параметра в направлении возрастания параметра 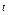 . . | |||
Вычислить интеграл по замкнутому контуру 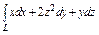 , если , если 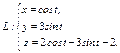 в направлении возрастания параметра в направлении возрастания параметра 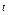 . . | Вычислить интеграл по замкнутому контуру 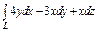 , если , если 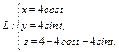 в направлении возрастания параметра в направлении возрастания параметра 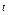 . . | Вычислить интеграл по замкнутому контуру 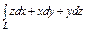 , если , если 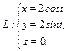 в направлении возрастания параметра в направлении возрастания параметра 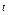 . . | |||
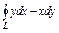 , где LOA – дуга эллипса , где LOA – дуга эллипса 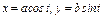 «пробегаемая»против хода часовой стрелки. «пробегаемая»против хода часовой стрелки. | Вычислить интеграл по замкнутому контуру 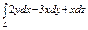 , если , если 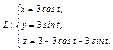 в направлении возрастания параметра в направлении возрастания параметра 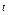 . . | 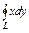 , где L – контур треугольника, образованного прямыми , где L – контур треугольника, образованного прямыми 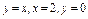 при положительном направлении обхода контура. при положительном направлении обхода контура. | |||
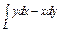 , где L – дуга эллипса , где L – дуга эллипса 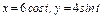 при положительном направлении обхода контура. при положительном направлении обхода контура. | 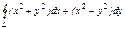 , где L – контур треугольника с вершинами , где L – контур треугольника с вершинами 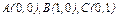 при положительном направлении обхода контура. при положительном направлении обхода контура. | 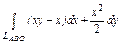 , где LАВО – ломаная , где LАВО – ломаная 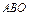 ( (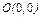 ; ; 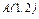 ; ; 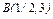 ) при положительном направлении обхода контура. ) при положительном направлении обхода контура. | |||
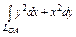 , где L – эллипс , где L – эллипс 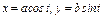 , «пробегаемый»по ходу часовой стрелки. , «пробегаемый»по ходу часовой стрелки. | 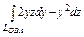 , где LOBA – ломаная , где LOBA – ломаная 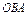 ; ; 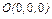 ; ; 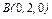 ; ; 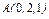 . . | 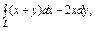 где L – контур треугольника с вершинами где L – контур треугольника с вершинами 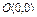 , , 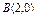 и и 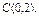 |
Задача 5. Найти работу силы 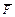 при перемещении вдоль линии
при перемещении вдоль линии 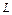 от точки
от точки 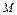 к точке
к точке 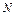 .
.
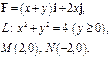 | 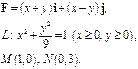 | 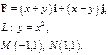 | |||
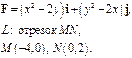 | 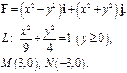 | 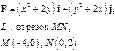 | |||
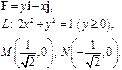 | 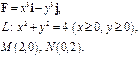 | 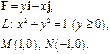 | |||
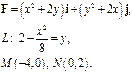 | 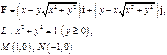 | 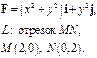 | |||
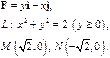 | 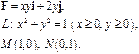 | 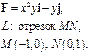 | |||
 | 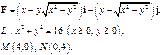 | 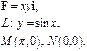 | |||
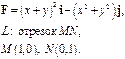 | 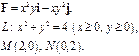 | 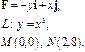 | |||
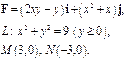 | 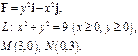 | 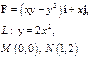 | |||
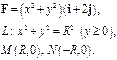 | 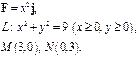 | 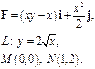 | |||
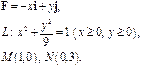 | 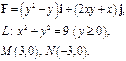 | 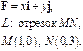 |
Задача 6. Вычислить поверхностные интегралы по площади поверхности (I рода)
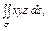 где σ - часть плоскости где σ - часть плоскости 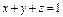 , лежащая в первом октанте; , лежащая в первом октанте; | 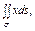 где σ – часть сферы где σ – часть сферы 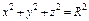 , лежащая в первом октанте; , лежащая в первом октанте; | 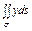 где σ – полусфера где σ – полусфера 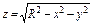 ; ; | |||
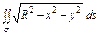 где σ – полусфера где σ – полусфера 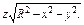 | 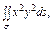 где σ – полусфера где σ – полусфера 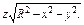 | 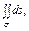 где σ – часть плоскости где σ – часть плоскости 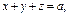 расположенная в первом октанте; расположенная в первом октанте; | |||
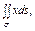 где σ – полусфера где σ – полусфера 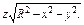 | 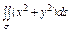 ,где σ – поверхность, отсекаемая от параболоиды ,где σ – поверхность, отсекаемая от параболоиды 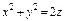 плоскостью плоскостью 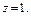 | 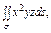 где σ – часть плоскости где σ – часть плоскости 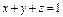 , лежащая в первом октанте; , лежащая в первом октанте; | |||
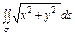 где σ – часть поверхности конуса где σ – часть поверхности конуса 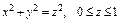 ; ; | 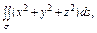 где σ – сфера где σ – сфера 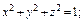 | 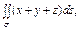 где σ – часть сфера где σ – часть сфера 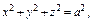 лежащая в первом октанте; лежащая в первом октанте; | |||
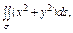 где σ – часть конической поверхности где σ – часть конической поверхности 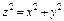 , заключенной между плоскостями , заключенной между плоскостями 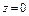 и и 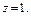 | 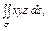 где σ – часть поверхности где σ – часть поверхности 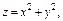 расположенная между плоскостями расположенная между плоскостями 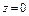 и и 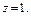 | 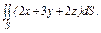 где S – часть плоскости (p), отсеченная координатными плоскостями где S – часть плоскости (p), отсеченная координатными плоскостями 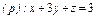 . . | |||
. 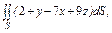 где S – часть плоскости (p), отсеченная координатными плоскостями. где S – часть плоскости (p), отсеченная координатными плоскостями. 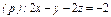 | 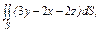 где S – часть плоскости (p), отсеченная координатными плоскостями где S – часть плоскости (p), отсеченная координатными плоскостями 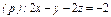 | 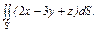 где S – часть плоскости (p) где S – часть плоскости (p) 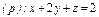 , отсеченная координатными плоскостями. , отсеченная координатными плоскостями. | |||
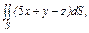 где S – часть плоскости (p), лежащая в первом октанте где S – часть плоскости (p), лежащая в первом октанте 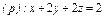 | . 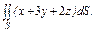 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 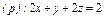 . . | 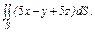 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 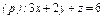 . . | |||
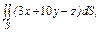 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 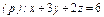 . . | 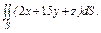 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 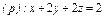 . . | 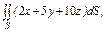 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 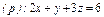 | |||
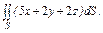 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 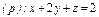 . . | 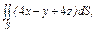 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 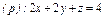 . . | 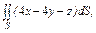 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 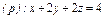 . . | |||
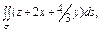 где σ – часть плоскости где σ – часть плоскости 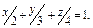 лежащая в первом октанте; лежащая в первом октанте; | 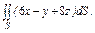 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 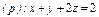 | 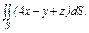 часть плоскости (p), лежащая в первом октанте часть плоскости (p), лежащая в первом октанте 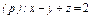 |
Задача 7. Вычислить поверхностные интегралы по координатам (II рода)
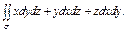 где σ – положительная сторона куба, составленного плоскостями где σ – положительная сторона куба, составленного плоскостями 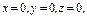 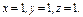 | 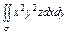 где σ – положительная сторона нижней половины сферы где σ – положительная сторона нижней половины сферы 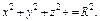 | ||
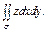 где σ – внешняя сторона эллипсоида где σ – внешняя сторона эллипсоида 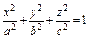 . . | 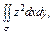 где σ – внешняя сторона эллипсоида где σ – внешняя сторона эллипсоида 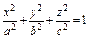 . . | ||
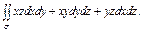 где σ – внешняя сторона пирамиды, составленной плоскостями где σ – внешняя сторона пирамиды, составленной плоскостями 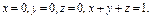 | 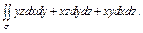 где σ – внешняя сторона поверхности, расположенной в первом октанте и составленной из цилиндра где σ – внешняя сторона поверхности, расположенной в первом октанте и составленной из цилиндра 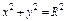 и плоскостей и плоскостей 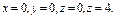 | ||
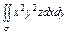 ,где σ – внешняя сторона верхней половины сферы ,где σ – внешняя сторона верхней половины сферы 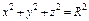 | 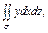 где σ – верхняя сторона части плоскости где σ – верхняя сторона части плоскости 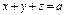 , лежащей в первом октанте; , лежащей в первом октанте; | ||
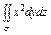 , где σ - внешняя сторона части поверхности параболоиды , где σ - внешняя сторона части поверхности параболоиды 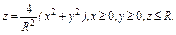 | 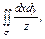 где σ - внешняя сторона сферы где σ - внешняя сторона сферы 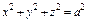 | ||
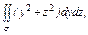 где σ - внешняя сторона части параболоиды где σ - внешняя сторона части параболоиды 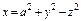 , отсечённой плоскостью , отсечённой плоскостью 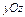 . . | 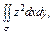 где σ – внешняя сторона полусферы где σ – внешняя сторона полусферы 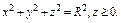 | ||
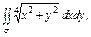 где σ - нижняя сторона круга где σ - нижняя сторона круга 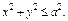 | 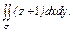 где σ – внешняя сторона полусферы где σ – внешняя сторона полусферы 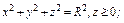 | ||
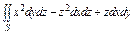 , где S – часть поверхности параболоида , где S – часть поверхности параболоида 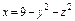 (нормальный вектор n которой образует острый угол с ортом k), отсекаемая плоскостью (нормальный вектор n которой образует острый угол с ортом k), отсекаемая плоскостью 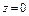 . . | 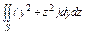 , где S – часть поверхности параболоида , где S – часть поверхности параболоида 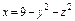 (нормальный вектор n которой образует острый угол с ортом i), отсеченная плоскостью (нормальный вектор n которой образует острый угол с ортом i), отсеченная плоскостью 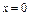 . . | ||
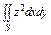 , где S – внешняя сторона поверхности эллипсоида , где S – внешняя сторона поверхности эллипсоида 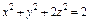 . . | 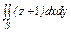 , где S – внешняя сторона поверхности сферы , где S – внешняя сторона поверхности сферы 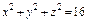 . . | ||
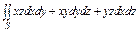 , где S – верхняя часть плоскости , где S – верхняя часть плоскости 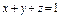 , отсеченной координатными плоскостями. , отсеченной координатными плоскостями. | 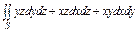 , где S – верхняя сторона плоскости , где S – верхняя сторона плоскости 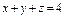 , отсеченной координатными плоскостями. , отсеченной координатными плоскостями. | ||
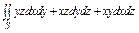 , где S – наружная поверхность цилиндра , где S – наружная поверхность цилиндра 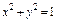 , отсеченная плоскостями , отсеченная плоскостями 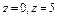 . . | 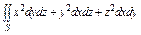 , где S – внешняя сторона сферы , где S – внешняя сторона сферы 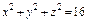 , лежащая в первом октанте. , лежащая в первом октанте. | ||
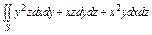 , где S – часть поверхности параболоида , где S – часть поверхности параболоида 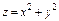 (нормальный вектор n которой образует острый угол с ортом k), вырезаемая цилиндром (нормальный вектор n которой образует острый угол с ортом k), вырезаемая цилиндром 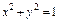 . . | 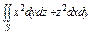 , где S – часть поверхности конуса , где S – часть поверхности конуса 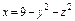 (нормальный вектор n которой образует тупой угол с ортом k), лежащая между плоскостями (нормальный вектор n которой образует тупой угол с ортом k), лежащая между плоскостями 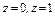 . . | ||
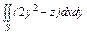 , где S – часть поверхности параболоида , где S – часть поверхности параболоида 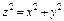 (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостью (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостью 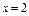 . . | 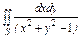 , где S – часть поверхности гиперболоида , где S – часть поверхности гиперболоида 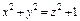 (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостями (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостями 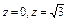 . . | ||
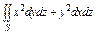 , где S – часть поверхности параболоида , где S – часть поверхности параболоида 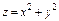 (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостью (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостью 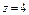 . . | 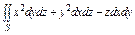 , где S – часть поверхности конуса , где S – часть поверхности конуса 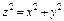 (нормальный вектор n которой образует острый угол с ортом k), отсекаемая плоскостями (нормальный вектор n которой образует острый угол с ортом k), отсекаемая плоскостями 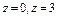 . . | ||
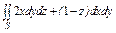 , где S – внутренняя сторона цилиндра , где S – внутренняя сторона цилиндра 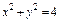 , отсекаемая плоскостями , отсекаемая плоскостями 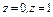 . . | 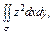 где σ – внешняя сторона части эллипсоида где σ – внешняя сторона части эллипсоида 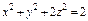 , лежащая в первом октанте. , лежащая в первом октанте. |
 2015-07-14
2015-07-14 3319
3319







