Теорема Веерштрасса

Пусть дана непрерывная числовая функция, определённая на отрезке, то есть 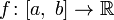и 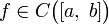. Пусть

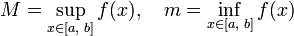
— точные верхняя и нижняя грани множества значений функции f соответственно. Тогда эти значения конечны (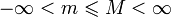) и достигаются (существуют такие, что ).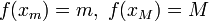

Билет 15

Двойственность в математическом программировании ( МП), как и вообще в математике, играет фундаментальную роль. Она выступает в качестве краеугольного камня соответствующих теорий, порождает арсенал конструктивных средств анализа математических моделей, построения эффективных алгоритмов решения задач и формальной оценки этой эффективности.

Если - некоторый исходный математический объект (модель), то двойственный объект, вообще говоря, выступает как некий внешний по отношению к объект ''наблюдения'' за. Конечно, двойственность в зависимости от ее конкретного содержания, определяемого конкретной математической дисциплиной (алгебра, функциональный анализ, выпуклый анализ, теория оптимального управления и т.д.), несет в себе следы специфики соответствующей дисциплины. Но именно это обстоятельство и превращает двойственность в математике в здание хотя в определенном смысле и единой, но гармонически организованной и насыщенной архитектуры.

Содержание двойственности в математическом программировании состоит в сопоставлении исходной задаче C другой задачи, формируемой по определенным правилам и называемой двойственной. Эти задачи связаны математически содержательными соотношениями, позволяющими, например, получить оценки критериальной эффективности всех параметров, формирующих задачу C; свести решение оптимизационной задачи к решению некоторой системы неравенств; сформировать в изящной форме условия оптимальности; оценить скорость сходимости итерационных процессов для задачи C и т.д.

Если задача МП (или ЛП) - результат моделирования конкретной экономической (производственной) ситуации, то двойственность и та информация, которую двойственность порождает, позволяют провести глубокий анализ моделируемой ситуации (моделируемого объекта), выявить узкие места, тенденции динамики объекта, выразив эти факторы в количественной форме. За такого рода анализом закрепился термин - экономико-математический анализ. Профессионально сделанные пакеты прикладных программ (ППП), решающие задачи МП или ЛП, обычно выдают в форме удобных распечаток всю совокупность информации, необходимую для экономико-математического анализа. Это дает экономистам хорошие возможности для оценки состояния экономических (или производственных) систем и идентификации параметров управления.

Ниже конспективно излагается материал по двойственности для различных классов задач МП (преимущественно линейных), а именно: стандартных задач ЛП, несобственных, лексикографических, паретовских, дизъюнктивных и др.

Билет 19

Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:

f(x) -> min,

x принадлежит [a, b].

Максимизация целевой функции эквивалента минимизации (f(x) -> max) эквивалентна минимизации противоположной величины (-f(x) -> min), поэтому, не умаляя общности можно рассматривать только задачи минимизации.

К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того, необходимость в минимизации функций одной переменной возникает при реализации некоторых методов решения более сложных задач оптимизации.

Для решения задачи минимизации функции f(x) на отрезке [a, b] на практике, как правило, применяют приближенные методы. Они позволяют найти решения этой задачи с необходимой точностью в результате определения конечного числа значений функции f(x) и ее производных в некоторых точках отрезка [a, b]. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.

Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f(x) в заданных точках.

Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию f(x) унимодальной на отрезке [a, b].

Метод перебора

Метод поразрядного поиска

Метод деления попалам

Метод золотого сечения

Билет 23