2015-07-21
989
Сущность принципа Лагранжа состоит в преобразовании задач с ограничениями к ряду задач более простой структуры (в большинстве случаев – к задачам без ограничений).
1. Рассмотрим принцип Лагранжа на примере конечномерных задач с ограничениями типа равенств.
Пусть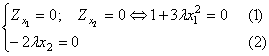 
; 
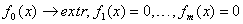(3) где 
.
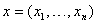Ограничение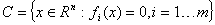 
задается системой равенств.
Функционал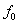 
и функции 
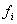, задающие уравнения связи 
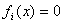, предполагаются непрерывно дифференцируемыми (т.е. все их частные производные первого порядка непрерывны).
Воспользуемся правилом Лагранжа для решения задачи (3). Для этого:
1) Составим функцию Лагранжа
Числа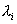 
- называют множителями Лагранжа. Причем, функция, экстремум которой ищется, также должна быть домножена на неопределенный множитель. Если этого не сделать, то правило Лагранжа может оказаться неверным.
2) Выпишем необходимые условия экстремума
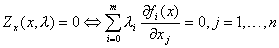
3) Найдем стационарные точки из полученных n – уравнений, дополненных m – уравнениями связи.
В подобных случаях говорят о полноте набора условий для определения стационарных точек.
Причем, не все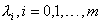 
равны нулю.
В задаче на min можно положить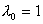 
или другой положительной константе. В задаче на max – равным минус единице или любой другой положительной константе.
Билет 9
