Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны 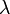 и характерным размером неоднородностей среды
и характерным размером неоднородностей среды 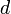 , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае дифракции проявляет себя в виде эффекта рассеяния волн.[1]
, либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае дифракции проявляет себя в виде эффекта рассеяния волн.[1]
Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.
Дифракция волн может проявляться:
§ в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении;
§ в разложении волн по их частотному спектру;
§ в преобразовании поляризации волн;
§ в изменении фазовой структуры волн.
Тонкости в толковании термина «дифракция»
В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её.
Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка).
Исходное ограничение волнового поля в пространстве и его определённая структура могут возникнуть не только за счёт присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.
Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции.
Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на непоглощающих (прозрачных), так называемых фазовых, структурах.
Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то наблюдается тенденция понимать её проявление как любое отступление от законов геометрической оптики.
При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является.
Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.
Ещё один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).
Раздел оптики «Оптика кристаллов», имеющей дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции. В то же самое время он нуждается в корректировке используемых представлений геометрической оптики. Это связано с различием в понятии луча (как направления распространения света) и распространения волнового фронта (то есть направления нормали к нему)
Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.
Частные случаи дифракции
Исторически в проблеме дифракции сначала рассматривались два крайних случая, связанных с ограничением препятствием (экраном с дыркой) сферической волны и это была дифракция Френеля, либо плоской волны на щели или системе отверстий - дифракция Фраунгофера
 2015-07-21
2015-07-21 1578
1578