Интеграл Лагранжа является интегралом движения идеальной баротропной среды для потенциального течения (установившегося или неустановившегося); он имеет вид:
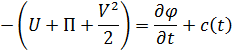
В последнем равенстве 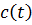 является функцией, не зависящей от координат, но в общем случае зависящая от времени.
является функцией, не зависящей от координат, но в общем случае зависящая от времени.
Очевидно, что каждое слагаемое в уравнении Лагранжа имеет размерность 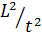 .
.
Из уравнения Лагранжа следует, что при потенциальном течении полная энергия единицы массы не зависит от координат, т.е. в данный момент времени есть величина постоянная для всех точек в потоке.
Функцию 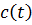 можно исключить из уравнения Лагранжа, применив его для двух любых точек в потоке, взятых при одном и том же ориентированном моменте времени
можно исключить из уравнения Лагранжа, применив его для двух любых точек в потоке, взятых при одном и том же ориентированном моменте времени
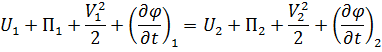
Если жидкость несжимаемая, а из объемных сил действует только сила тяжести, то направив ось z вертикально вверх, получим 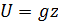 и интеграл Лагранжа примет вид:
и интеграл Лагранжа примет вид:
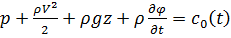 ,
,
где 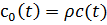
 2015-07-21
2015-07-21 598
598








