2015-07-21
593
Интегрируем уравнение Эйлера при следующих допущениях:
1. Движение установившееся.
2. Массовые силы, действующие на жидкость имеют потенциал.
3. Жидкость баротропна, т.е.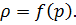 
При установившемся движении линии тока совпадают с траекториями частиц. Поэтому, например, проекция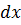 
перемещения частицы жидкости 
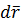вдоль элементарной струйки за время 
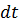равна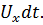 
С целью интегрирований уравнений движения идеальной жидкости
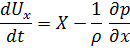
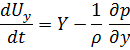
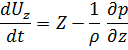
Умножим на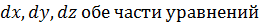 
(Д) соответственно и сложим отдельно левы и правые части.
Левую часть, полученную в результате сложения, преобразуем так:
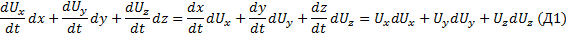
Заметим для дальнейших преобразований следующее:
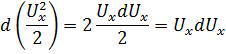
Тогда левая часть будет иметь вид:
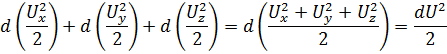
Так как движение установившееся, то давление не зависит от времени:
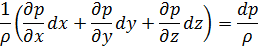
Так как массовые силы имеют потенциал, то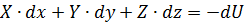 
Если массовой силой является сила тяжести, то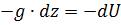 
В результате преобразованное выражение принимает вид:
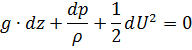
В частности, для несжимаемой жидкости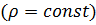 
:
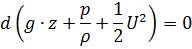
Производя формальное интегрирование последнего выражения получим:
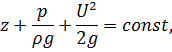
т.е. сумма трех слагаемых в левой части последнего равенства (интеграла Бернулли) сохраняет постоянное значение вдоль элементарной струйки.
Если на данной элементарной струйке выбрать два сечения, то для них возможно записать:
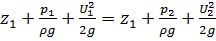(Y1)
Это равенство называется уравнением Бернулли для элементарной струйки идеальной жидкости. (так как на сечение элементарной струйки не накладывается никаких ограничений, его возможно выбрать прямоугольным со сторонами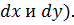 
Так как скорость и давление по течению элементарной струйки не меняются, то уравнение (Y1) справедливо для линии тока.
Несмотря на то, что удельная энергия жидкости в элементарной струйке имеет конечное значение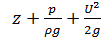 
, ее полная энергия:
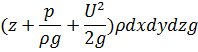
в любом сечении бесконечно мала.
