При выводе уравнений Эйлера все слагаемые были поделены на 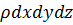 , а при выводе уравнения Бернулли еще и на
, а при выводе уравнения Бернулли еще и на 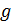 – т.е. каждое слагаемое в уравнении Бернулли представляет собой энергию некоторого объема жидкости, поделенную на вес этого объема.
– т.е. каждое слагаемое в уравнении Бернулли представляет собой энергию некоторого объема жидкости, поделенную на вес этого объема.
Потенциальная и кинетическая энергия элементарного объема жидкости равны соответственно:

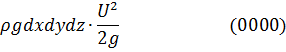
Энергия, обусловленная давлением, выражается так:
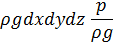
Из механики известно, что потенциальная энергия тела 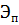 в силы тяжести равна произведению веса частицы
в силы тяжести равна произведению веса частицы 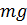 на высоту ее поднятия
на высоту ее поднятия 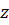 , которая отсчитывается от некоторой горизонтальной плоскости т.е.
, которая отсчитывается от некоторой горизонтальной плоскости т.е.
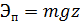
Кинетическая энергия частицы определяется как:
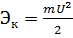 ,
,
Где U – скорость частицы, m – ее масса.
Энергия, отнесенная к единице веса тела, называется удельной энергией; поэтому, разделив 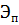 и
и 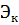 на вес
на вес 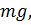 получим:
получим:
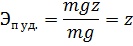
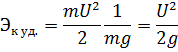
Аналогично для жидкости, удельная потенциальная энергия положения равна z, имеет размерность длины и называется геометрической высотой. Удельная энергия, обусловленная давлением, равная 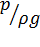 также имеет размерность длины и называется высотой. Удельная кинетическая энергия равна
также имеет размерность длины и называется высотой. Удельная кинетическая энергия равна 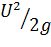 и называется высотой скоростного напора.
и называется высотой скоростного напора.
|
|
|
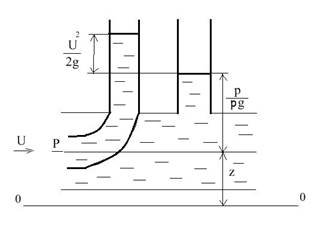
Геометрический смысл каждого слагаемого в уравнении Бернулли приведен на рис.1
Чтобы пояснить физический смысл величины 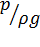 представим элементарную струйку и сечение её
представим элементарную струйку и сечение её 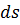 , в котором скорость равна U, а давление
, в котором скорость равна U, а давление 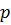 . Частицы жидкости, расположенные в этом сечении за время
. Частицы жидкости, расположенные в этом сечении за время 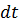 перенесутся на расстояние
перенесутся на расстояние 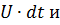 работа сил давления
работа сил давления 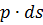 на этом пути будет равна
на этом пути будет равна 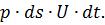
 2015-07-21
2015-07-21 778
778








