Необходимые условия оптимальности

Правило множителей Лагранжа

Задача условной оптимизации формулируется следующим образом:

f (x) = f (x ₁, x ₂,..., x _n) Þextr,

(1.9)

j _i (x) = j _i(x ₁, x ₂,..., x _n) = 0, 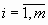, m < n.

(1.10)

Необходимые условия локальной оптимальности для этой задачи известны как правило множителей Лагранжа и формулируются по отношению к функции Лагранжа

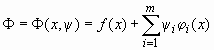
(1.11)

(где y _j – множители Лагранжа), а именно: если x* – локальное решение задачи (1.9), (1.10), то существует вектор 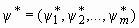такой, что

,

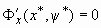(1.12)

где 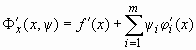– вектор производных от функции Лагранжа по компонентам вектора х.

Любая точка x*, удовлетворяющая при некотором y* условиям (1.12), а также условиям допустимости (1.10), называется стационарной точкой задачи (1.9), (1.10). Как и в случае безусловной задачи оптимизации, стационарные точки не обязаны быть решениями задачи (1.9), (1.10). Здесь также существуют достаточные условия оптимальности с привлечением вторых производных.