КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
И ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ 0
НАРАЩЕНИЕ И ДИСКОНТИРОВАНИЕ ПО ПРОСТОЙ ПРОЦЕНТНОЙ СТАВКЕ
1.1. Краткие сведения, необходимые для выполнения
задания № 1
Наращение по простым процентам означает, что проценты начисляются на первоначальную сумму долга. Обычно используются при выдаче краткосрочных ссуд или когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору.
Формула наращенной суммы:
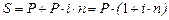 , (1.1)
, (1.1)
где I – проценты за весь срок ссуды, P – первоначальная сумма долга, S – наращенная сумма, или сумма в конце срока, i – ставка наращения, n – срок ссуды.
Причем, если срок выражен в годах, то n=n, если срок выражен в месяцах (например t месяцев), то 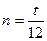 , если же срок выражен в днях, то
, если же срок выражен в днях, то 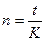 , где t – количество дней, а К – временная база (число дней в году). K может быть равным 360 дням (тогда получают обыкновенные или коммерческие проценты), 365 дням, 366 дням (точные проценты).
, где t – количество дней, а К – временная база (число дней в году). K может быть равным 360 дням (тогда получают обыкновенные или коммерческие проценты), 365 дням, 366 дням (точные проценты).
Дисконтирование по простой процентной ставке – процесс, обратный наращению по простым процентам. Задача в этом случае формулируется так: какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i:
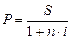 . (1.2)
. (1.2)
Установленная таким путем величина P называется современной величиной суммы S, которая будет выплачена спустя n лет.
Величина
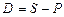 (1.3)
(1.3)
(удержанные проценты) называется дисконтом.
Часто требуется рассчитать срок ссуды. В этом случае задача может формулироваться следующим образом: на какой промежуток времени следует положить сумму P под простые проценты i, чтобы получить в конечном итоге сумму S. Или же необходимо найти проценты, под которые необходимо положить P, чтобы через срок, равный n получить S.
Рассмотрим наиболее распространенные задачи наращения и дисконтирования по простым процентам.
2. КОНТУР ФИНАНСОВОЙ ОПЕРАЦИИ. ПОГАШЕНИЕ ЗАДОЛЖЕННОСТИ ЧАСТЯМИ С ПОМОЩЬЮ АКТУАРНОГО МЕТОДА
2.1. Краткие сведения, необходимые для выполнения
задания № 2
|
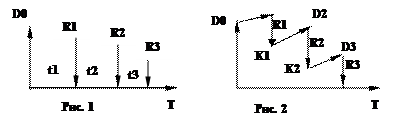 |
Сбалансированная операция обязательно имеет замкнутый контур, то есть последняя выплата полностью покрывает остаток задолженности.
Краткосрочные обязательства погашаются иногда с помощью последовательности частичных платежей. В этом случае надо решить вопрос о том, какую сумму надо брать за базу для расчета процентов и каким путем определять остаток задолженности. Одним из методов решения этой задачи является актуарный метод. Этот метод применяется в основном в операциях со сроком более одного года.
Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга. Частичный платеж идет в первую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму начисленных процентов, то разница идет на погашение основной суммы долга. Непогашенный остаток долга служит базой для начисления процентов за следующий период и т.д. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Такое поступление приплюсовывается к следующему платежу. В дальнейшем мы будем выплачивать суммы, большие начисленных процентов. В дальнейшем мы будем выплачивать платежи, большие начисляемых процентов.
Для случая, показанного на рис. 2, получим следующие расчетные формулы:
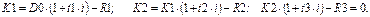
 2015-07-21
2015-07-21 996
996







