Задача Коши ставиться так. Найти функцию 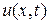 , удовлетворяющую уравнению
, удовлетворяющую уравнению
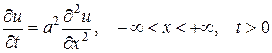 (1)
(1)
и начальному условию
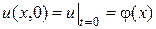 , (2)
, (2)
Такая математическая модель используется в ситуациях, когда режим на границе области не оказывает существенного влияния на развитие процесса в средней части.
Решение задачи (1) – (2) даётся формулой Пуассона
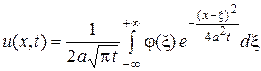 . (3)
. (3)
Функция (функция Грина)
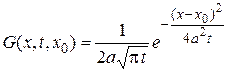 , (4)
, (4)
входящая в формулу Пуассона называется фундаментальным решением уравнения теплопроводности и является решением задачи Коши
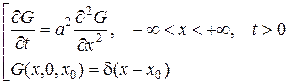 (5)
(5)
где 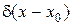 – дельта функция Дирака, которая определяется формально при помощи соотношений:
– дельта функция Дирака, которая определяется формально при помощи соотношений:
1. 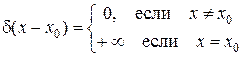 .
.
2. 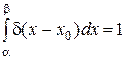 на любом интервале
на любом интервале 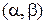 , содержащем точку
, содержащем точку 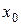 .
.
Основным свойством 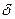 – функции является следующее: если
– функции является следующее: если 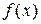 непрерывная функция, то
непрерывная функция, то
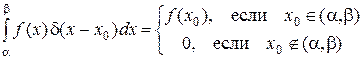 .
.
Задача (5) моделирует ситуации, когда в начальный момент времени в точке 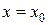 имеется мгновенный сосредоточенный источник тепла (точечный тепловой импульс) в одномерном теплопроводящем теле (стержне); или происходит мгновенное вспрыскивание «погонной единицы» диффундирующего вещества в тонкую трубку заполненную другим веществом.
имеется мгновенный сосредоточенный источник тепла (точечный тепловой импульс) в одномерном теплопроводящем теле (стержне); или происходит мгновенное вспрыскивание «погонной единицы» диффундирующего вещества в тонкую трубку заполненную другим веществом.
График функции (4) – решения задачи (5) при любом 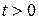 называется кривой Гаусса (рис).
называется кривой Гаусса (рис).
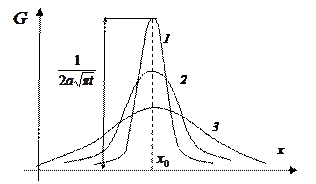 | Кривые 1, 2, 3 соответствуют моментам времени 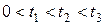 . График функции . График функции 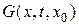 при любом значении при любом значении 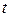 симметричен относительно прямой симметричен относительно прямой 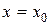 . Максимум достигается при . Максимум достигается при 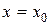 , и он равен , и он равен 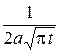 . . |
Из графика видно, что после мгновенного импульса температура в стержне (или концентрация в тонкой трубке) выравнивается.
Свойства функции Грина:
1. 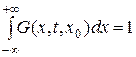 .
.
(площади под кривыми равны единицы)
2. 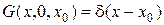 .
.
3. 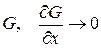 при
при 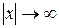 .
.
С помощью функции Грина решение (3) задачи (1) – (2) можно представить в виде
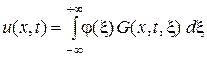 .
.
и можно рассматривать как результат суперпозиции решений, возникающих в точке 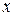 в момент времени
в момент времени 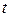 вследствие непрерывно распределенных по длине стержня (или трубки) тепловых импульсов (источников диффундирующего вещества) интенсивности
вследствие непрерывно распределенных по длине стержня (или трубки) тепловых импульсов (источников диффундирующего вещества) интенсивности 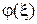 в точке
в точке 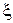 , приложенных в момент
, приложенных в момент 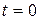 .
.
 2015-07-14
2015-07-14 2037
2037







