В общем виде линейное дифференциальное уравнение с частными производными и постоянными коэффициентами можно представить в виде:
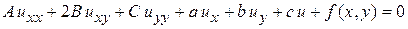 , (1)
, (1)
где 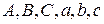 – постоянные,
– постоянные, 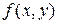 – заданная функция двух переменных.
– заданная функция двух переменных.
Для определения вида этого уравнения и приведения к канонической форме по-прежнему надо составить характеристические уравнения, которые в этом можно проинтегрировать:
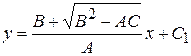 ,
, 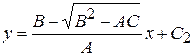 .
.
А) Если 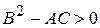 , то уравнение (1) принадлежит к гиперболическому виду, и вводя обозначение
, то уравнение (1) принадлежит к гиперболическому виду, и вводя обозначение 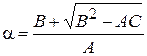 ,
, 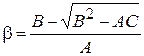 , получим два семейства характеристик
, получим два семейства характеристик
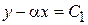 и
и 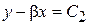 .
.
Вводя новые переменные 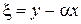 ,
, 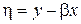 получим канонический вид уравнения (1):
получим канонический вид уравнения (1):
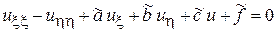 (2)
(2)
или
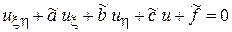 . (2’)
. (2’)
Б) Если 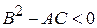 , то уравнение (1) принадлежит к эллиптическому виду, и, вводя обозначение
, то уравнение (1) принадлежит к эллиптическому виду, и, вводя обозначение 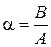 ,
, 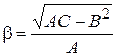 , получим два семейства комплексно-сопряженных характеристик
, получим два семейства комплексно-сопряженных характеристик
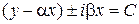 .
.
Вводя новые переменные 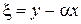 ,
, 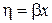 получим канонический вид уравнения (1):
получим канонический вид уравнения (1):
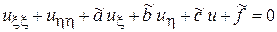 . (3)
. (3)
В) Если 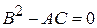 , то уравнение (1) принадлежит к параболическому виду, обозначая
, то уравнение (1) принадлежит к параболическому виду, обозначая 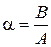 получим семейство характеристик
получим семейство характеристик 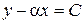 . Вводя новые переменные
. Вводя новые переменные
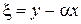 ,
, 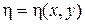 ,
,
где 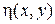 – произвольная функция, удовлетворяющая условию
– произвольная функция, удовлетворяющая условию 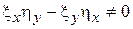 , получим каноническую форму для уравнения (1):
, получим каноническую форму для уравнения (1):
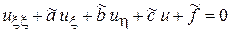 . (4)
. (4)
Для дальнейшего упрощения уравнений (2) или (2’), (3), (4) вводим новую функцию 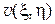 по формуле
по формуле 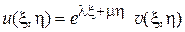 , где
, где 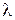 и
и 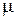 некоторые произвольные постоянные.
некоторые произвольные постоянные.
В результате преобразований, получаем:
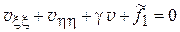 (5)
(5)
– каноническая форма для эллиптического уравнения;
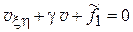 (6)
(6)
или
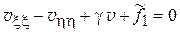 (6’)
(6’)
– канонические формы для гиперболического уравнения.
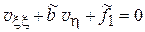 (7)
(7)
– каноническая форма для параболического уравнения.
Замечание.
Аналогичный признак принадлежности к тому или иному типу уравнения может быть положен в основу классификации линейных уравнений вида
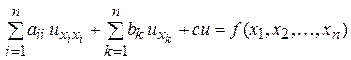 (**)
(**)
со многими независимыми переменными 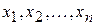 , где
, где 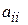 ,
, 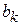 , с – постоянные коэффициенты.
, с – постоянные коэффициенты.
Уравнение (**) называется:
эллиптическим, если все коэффициенты 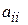 не равны нулю и имеют один и тот же знак;
не равны нулю и имеют один и тот же знак;
гиперболическим, если коэффициенты 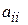 все не равны нулю, и все, кроме одного (например,
все не равны нулю, и все, кроме одного (например, 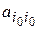 ), имеют один и тот же знак, а
), имеют один и тот же знак, а 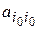 имеет противоположный знак;
имеет противоположный знак;
параболическим, если коэффициенты 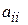 все, кроме одного (например,
все, кроме одного (например, 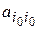 ), не равны нулю и имеют один и тот же знак, а
), не равны нулю и имеют один и тот же знак, а 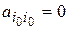 и
и 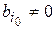 .
.
 2015-07-14
2015-07-14 1545
1545








