2015-07-14
919
Определение. Дифференциальным уравнением с частными производными называется уравнение связывающее независимые переменные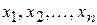 
, искомую функцию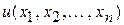 
и её частные производные
. (*)
(
).
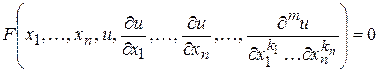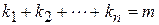Порядком дифференциального уравнения называется наивысший порядок входящих частных производных.
Определение. Решением дифференциального уравнения (*) в некоторой области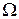 
называется любая функция 
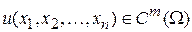, такая, что подстановка этой функции и её производных в уравнение (*) обращает его в тождество в области .
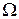Замечание. Запись 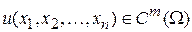обозначает, что функция 
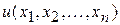принадлежит к классу непрерывных функций вместе с производными 
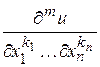в области .
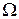Рассмотрим несколько простейших примеров.
Пример 1.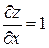 
, где 
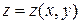
Интегрируя, получим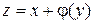 
, где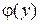 
– произвольная функция 
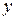.Это – общее решение данного дифференциального уравнения.
Пример 2.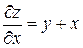 
, где
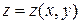
Интегрируя по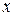 
, получим
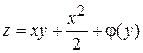, где 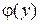– произвольная функция .
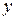Пример 3.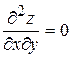 
, где .
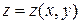Интегрируем уравнение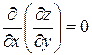 
по 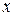, получаем 
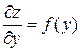, где 
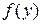– произвольная функция 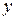. Интегрируя теперь по 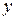, получим
,
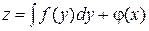где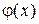 
– произвольная функция 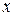. Или, обозначая 
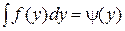, окончательно будем иметь 
.
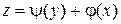Приведенные примеры наводят на мысль, что общее решение дифференциального уравнения в частных производных первого порядка зависит от одной произвольной функции, общее решение уравнения второго порядка зависит от двух произвольных функций, а общее решение уравнения р -го порядка, вероятно, зависит от р произвольных функций.
