Рассмотрим процедуру метода Фурье на примере решения смешанной задачи для уравнения теплопроводности в случае одной пространственной переменной.
Задача 1. Найти решение 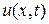 однородного уравнения
однородного уравнения
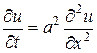 ,
, 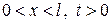 (1)
(1)
удовлетворяющее начальному условию
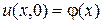 ,
, 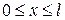 (2)
(2)
и нулевым (однородным) граничным условиям:
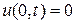 ,
, 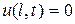 ,
, 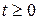 (3)
(3)
Суть метода состоит в том чтобы искать нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (3), в виде
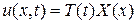 . (4)
. (4)
Подставляя (4) в (1), получим
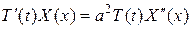
или
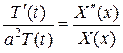 .
.
Поскольку левая часть уравнения является функцией только от 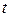 , а правая только от
, а правая только от 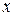 , то равенство возможно, если они равны постоянной:
, то равенство возможно, если они равны постоянной:
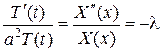 .
.
Отсюда получаем два обыкновенных дифференциальных уравнения:
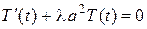 , (5)
, (5)
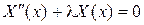 , (6)
, (6)
и функция 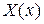 удовлетворяет условиям
удовлетворяет условиям 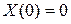 ,
, 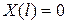 .
.
Таким образом, для определения функции 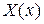 имеем задачу на собственные значения: найти те значения параметра
имеем задачу на собственные значения: найти те значения параметра 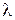 , при которых существуют нетривиальные решения задачи
, при которых существуют нетривиальные решения задачи
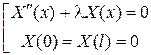 (7)
(7)
(задачи Штурма-Лиувилля).
Рассмотрим три случая, когда 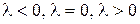 .
.
1. Пусть 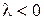 . Найдем решение дифференциального уравнения
. Найдем решение дифференциального уравнения 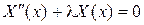 .
.
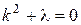 ,
, 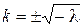 – два вещественных корня. Общее решение имеет вид
– два вещественных корня. Общее решение имеет вид
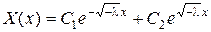 . Требование граничных условий означает:
. Требование граничных условий означает:
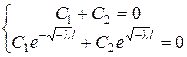 .
.
Определитель системы 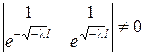 , следовательно,
, следовательно, 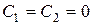 и при
и при 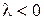 существуют только тривиальные решения
существуют только тривиальные решения 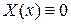 .
.
2. Пусть 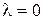 . Найдем решение дифференциального уравнения
. Найдем решение дифференциального уравнения 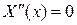 .
.
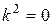 ,
, 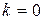 – один кратный корень. Общее решение имеет вид
– один кратный корень. Общее решение имеет вид
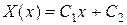 . Требование граничных условий означает:
. Требование граничных условий означает:
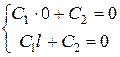 .
.
Откуда следует, что 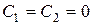 и при
и при 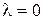 существуют только тривиальные решения
существуют только тривиальные решения 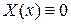 .
.
3. Пусть 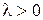 . Найдем решение дифференциального уравнения
. Найдем решение дифференциального уравнения 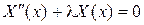 .
.
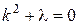 ,
, 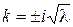 – два комплексно-сопряженных корня. Общее решение имеет вид
– два комплексно-сопряженных корня. Общее решение имеет вид
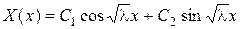 . Требование граничных условий означает:
. Требование граничных условий означает:
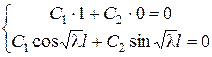 . (*)
. (*)
Система имеет нетривиальное решение тогда и только тогда, кода её определитель равен нулю 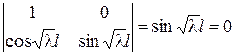 или
или 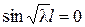 , следовательно,
, следовательно, 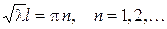 . Таким образом, нетривиальные решения задачи (7) возможны только если
. Таким образом, нетривиальные решения задачи (7) возможны только если
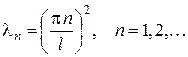 .
.
Из системы (*), получаем 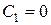 и, следовательно,
и, следовательно,
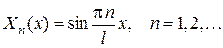
будут собственными функциями задачи Штурма-Лиувилля (7).
Собственные функции определены с точность до постоянного множителя 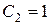 .
.
Перейдем к решению уравнения (5). При 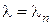 оно имеет вид
оно имеет вид
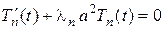
Решаем это уравнение разделением переменных 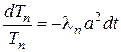 , откуда,
, откуда, 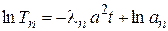 или
или
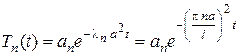 ,
,
где 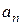 – произвольные постоянные. Таким образом, согласно (4) только функции
– произвольные постоянные. Таким образом, согласно (4) только функции
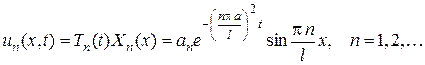 .
.
Удовлетворяют уравнению (1) и граничным условиям (3).
Образуем формальный ряд (как сумму решений)
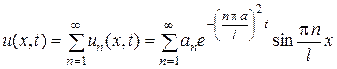 , (8)
, (8)
и потребуем, чтобы функция 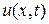 удовлетворяла начальному условию (2)
удовлетворяла начальному условию (2) 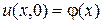 , получим
, получим
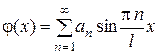 .
.
Полученный ряд представляет собой разложение функции 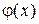 в ряд Фурье по синусам в интервале
в ряд Фурье по синусам в интервале 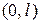 . Коэффициенты этого ряда определяются по известным формулам
. Коэффициенты этого ряда определяются по известным формулам
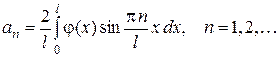 (9)
(9)
Итак, функция, определенная в виде ряда (8), коэффициенты которого определены формулами (9) есть решение поставленной задачи (1) – (3).
Задача 2.
Найти решение 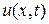 неоднородного уравнения теплопроводности
неоднородного уравнения теплопроводности
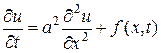 ,
, 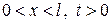 (10)
(10)
удовлетворяющее начальному условию
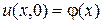 ,
, 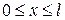 (11)
(11)
и нулевым (однородным) граничным условиям:
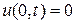 ,
, 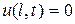 ,
, 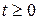 (12)
(12)
Предположим, что функция 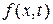 непрерывна, имеет непрерывную производную
непрерывна, имеет непрерывную производную 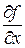 и для всех
и для всех 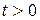 выполняется условие
выполняется условие 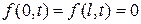 .
.
Решение задачи (10) – (12) будем искать в виде
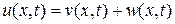 , (13)
, (13)
где 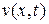 – есть решение задачи
– есть решение задачи
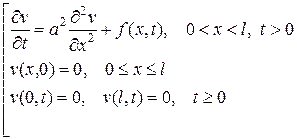 , (14)
, (14)
а функция 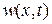 – есть решение задачи
– есть решение задачи
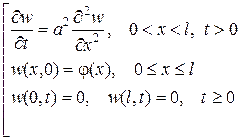 (15)
(15)
Задача (15)– это задача 1 и её решение известно.
Рассмотрим задачу (14). Будем искать её решение в виде ряда
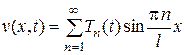 (16)
(16)
по собственным функциям 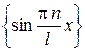 задачи соответствующей Штурма-Лиувилля (7)
задачи соответствующей Штурма-Лиувилля (7)
Подставим (16) в дифференциальное уравнение задачи (14)\, для этого найдем производные:
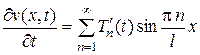 и
и 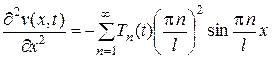 .
.
В результате подстановки получим
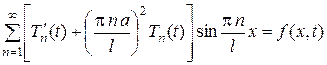 .
.
Разложим функцию 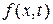 в ряд Фурье по синусам
в ряд Фурье по синусам
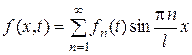 , где
, где 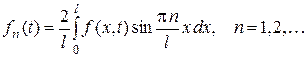
Тогда получим
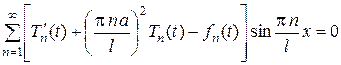 .
.
Отсюда следует,
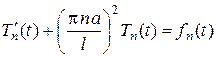 ,
, 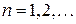
К полученным дифференциальным уравнениям надо добавить начальные условия задачи (14):
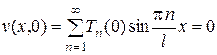 ,
, 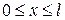
или
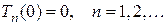
Решаем обыкновенное дифференциальное уравнение методом Бернулли.
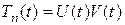 ,
, 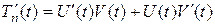 .
.
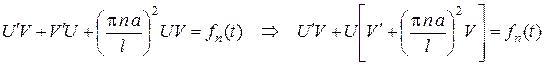 ,
, 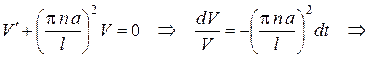
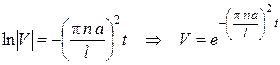 .
.
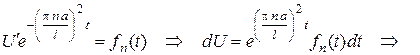
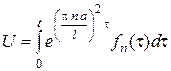 .
.
Тогда
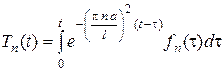 ,
, 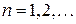 (17)
(17)
Подставляя (17) в (16), получим решение задачи (14)
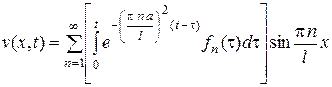 . (18)
. (18)
Функция 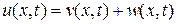 будет решением задачи 2.
будет решением задачи 2.
Задача 3.
Найти решение 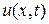 неоднородного уравнения
неоднородного уравнения
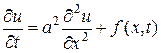 , (19)
, (19)
удовлетворяющее начальному условию
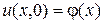 , (20)
, (20)
и неоднородным граничным условиям:
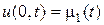 ,
, 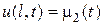 . (21)
. (21)
Введем новую неизвестную функцию 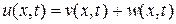 , где
, где
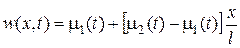 ,
,
Функцию 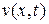 находим, как решение уравнения
находим, как решение уравнения
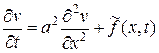 , где
, где 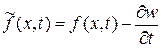 ,
,
с начальными условиями
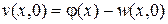 ,
,
и краевыми условиями
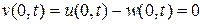 ,
, 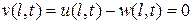 .
.
тогда решение сведется к задаче 2.
Для существования классического решения задачи 3, необходимо, чтобы функции 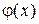 ,
, 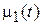 ,
, 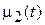 были непрерывными и выполнялись условия согласованности
были непрерывными и выполнялись условия согласованности 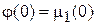 ,
, 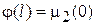 .
.
Для функции 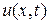 , непрерывной в замкнутой области справедлив принцип максимального значения.
, непрерывной в замкнутой области справедлив принцип максимального значения.
Теорема. Если функция 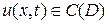 , удовлетворяет уравнению теплопроводности
, удовлетворяет уравнению теплопроводности 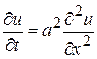 в точках области
в точках области 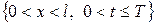 , то максимальное и минимальное значения функции
, то максимальное и минимальное значения функции 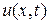 достигаются или в начальный момент времени
достигаются или в начальный момент времени 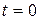 , или в точках границы на отрезке
, или в точках границы на отрезке 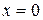 и
и 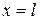 .
.
Из принципа максимума следуют две теоремы
Теорема. (единственности) Решение задачи 3 в прямоугольнике 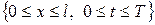 единственно.
единственно.
Теорема. Решение задачи 3 непрерывно зависит от начальных и граничных функций.
Пример.
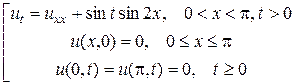
– это задача (14), в которой 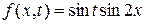 ,
, 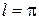 . Решение имеет вид:
. Решение имеет вид:
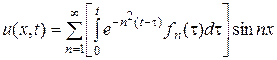 ,
,
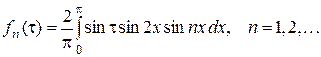 , следовательно
, следовательно
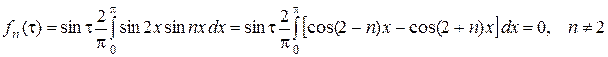 ,
,
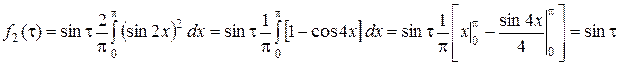 .
.
Тогда, 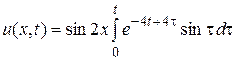
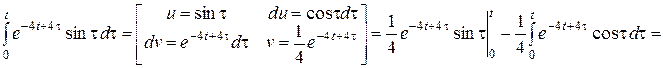
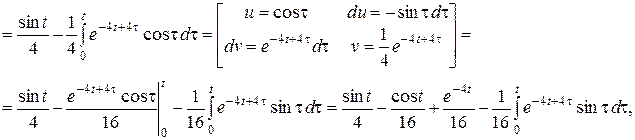
Отсюда, следует, 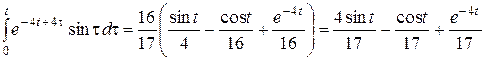 , и,
, и,
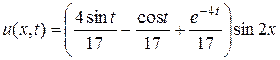 .
.
 2015-07-14
2015-07-14 10870
10870








