Основные уравнения математической физики и постановка задач для них

1. Волновое уравнение д ля функции :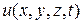

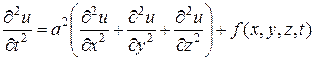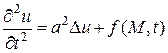или , (1)

где 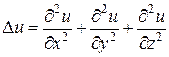– оператор Лапласа.

Волновое уравнение относится к гиперболическому типу. Уравнение (1), например, описывает процесс распространение механических возмущений в сплошной среде.

В одномерном случае волновое уравнение

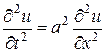
называют уравнением колебаний струны. Это уравнение описывает свободные колебания струны без воздействия внешних сил. Функция 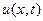характеризует вертикальное перемещение струны, 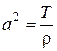, 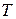– натяжение струны, 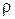– плотность материала струны.

2. У равнение Лапласа для функции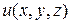

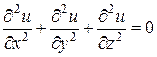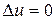или (2)

относится к уравнениям эллиптического типа. Этим уравнением, например, описывается стационарный процесс распределения тепла в однородной изотропной среде. Функция 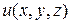– температура в точках среды.

Неоднородное уравнение

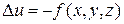(2’)

называется уравнением Пуассона.

3. Уравнение теплопроводности (уравнение диффузии) для функции :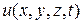

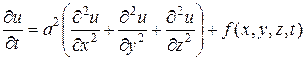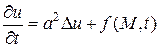или , (3)

относится к уравнениям параболического типа и описывает процесс распространения тепла в сплошной среде (а также лежит в основе математического моделирования диффузионных процессов).

Если в уравнениях (1), (3) в правой части функция 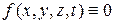, то они называются однородными, если 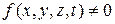, то уравнения (1) и (3) называются неоднородными.

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение, надо ещё знать начальное состояние этого процесса (начальное условие) в виде

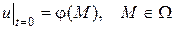(4)

или

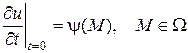(5)

и режим на границе области (граничное условие) в виде

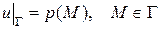(6)

или

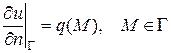. (7)

Здесь приняты обозначения 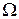– область, в которой происходит процесс, 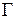– граница области, 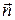– нормаль к границе области.

Различают три основных типа задач для дифференциальных уравнений математической физики (1) – (3).

1) Задача Коши для уравнений гиперболического и параболического типов (волнового уравнения и уравнения теплопроводности). В данной постановке задаются начальные условия, область 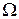совпадает со всем пространством, граничные условия отсутствуют.

2) Краевая задача для уравнения эллиптического типа (уравнения Лапласа, уравнения Пуассона). В такой постановке задаются граничные условия, начальные отсутствуют.

3) Смешанная задача для уравнений гиперболического и параболического типов (волнового уравнения и уравнения теплопроводности). Задаются начальные и граничные условия.