Рассмотрим некоторую область 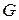 точек
точек 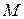 трехмерного пространства
трехмерного пространства 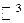 или плоскости (двумерного пространства)
или плоскости (двумерного пространства) 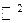 .
.
Область 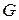 называется скалярным полем, если каждая точка
называется скалярным полем, если каждая точка 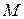 из этой области характеризуется определенным числом
из этой области характеризуется определенным числом 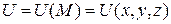 . Таким образом,
. Таким образом, 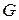 становится скалярным полем, если задается числовая функция
становится скалярным полем, если задается числовая функция 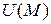 , для которой
, для которой 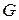 является областью определения.
является областью определения.
Область 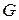 называется векторным полем, если каждая ее точка
называется векторным полем, если каждая ее точка 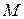 характеризуется вектором
характеризуется вектором 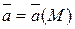 , исходящим их этой точки.
, исходящим их этой точки.
Векторное поле будет задано, если задать векторную функцию 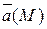 с областью определения
с областью определения 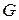 ,
, 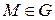 .
.
Задание векторного поля равносильно заданию трех числовых функций (в выбранной системе координат OXYZ с базисом 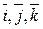 ), каждая из которых зависит от трех переменных:
), каждая из которых зависит от трех переменных:
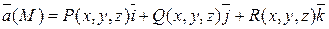 .
.
Если 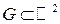 - плоская область, то скалярное поле задается функцией
- плоская область, то скалярное поле задается функцией 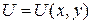 , а векторное поле имеет вид:
, а векторное поле имеет вид:
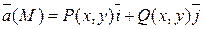 - поле плоское.
- поле плоское.
В дальнейшем будем считать, что функции 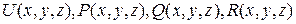 , а также
, а также 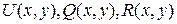 непрерывны в
непрерывны в 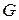 и имеют в этой области непрерывные частные производные первого порядка.
и имеют в этой области непрерывные частные производные первого порядка.
Df.1 Пусть 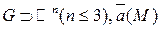 определена в
определена в 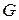 ,
, 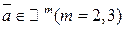 ,
, 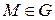 . Совокупность векторной функции
. Совокупность векторной функции 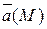 и области ее определения
и области ее определения 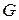 называется векторным полем. Т.е.:
называется векторным полем. Т.е.:
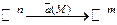 .
.
Если считать, что 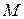 - конец радиуса вектора
- конец радиуса вектора 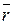 , то можно обозначить
, то можно обозначить 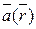 .
.
Если 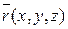 или
или 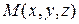 , то в координатной форме:
, то в координатной форме:
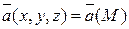 .
.
Df.2 Пусть 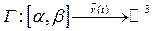 простая ориентированная спрямляемая кривая;
простая ориентированная спрямляемая кривая; 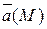 определена на
определена на 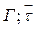 - единичный вектор касательной к кривой
- единичный вектор касательной к кривой 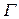 . Криволинейным интегралом по дуге
. Криволинейным интегралом по дуге 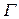 от векторной функции
от векторной функции 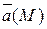 называется криволинейный интеграл I-го рода:
называется криволинейный интеграл I-го рода:
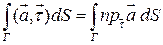 (1)
(1)
* Простая кривая 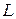 называется спрямляемой, если существует предел длин ломанных, вписанных в кривую при
называется спрямляемой, если существует предел длин ломанных, вписанных в кривую при 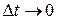 (этот предел называется длиной кривой
(этот предел называется длиной кривой 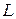 ). Аналогичные определения имеют место для пространственной кривой, заданной параметрически уравнениями в координатном пространстве OXYZ.
). Аналогичные определения имеют место для пространственной кривой, заданной параметрически уравнениями в координатном пространстве OXYZ.
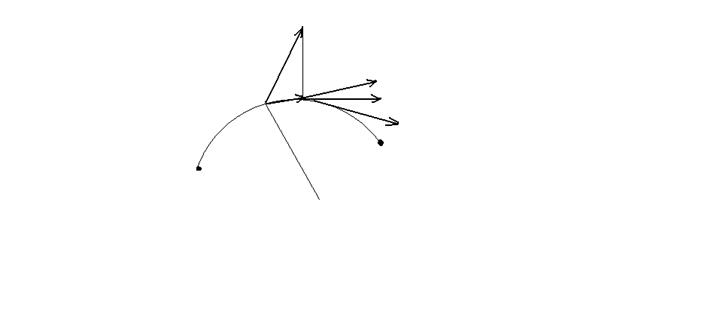
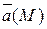
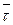
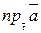
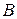
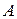
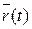
Векторными линиями векторного поля 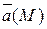 называются такие линии, у которых касательная в каждой точке направлена вдоль заданного в этой точке векторного поля.
называются такие линии, у которых касательная в каждой точке направлена вдоль заданного в этой точке векторного поля.
Пусть 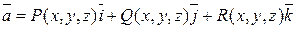 , а линия
, а линия 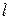 определена уравнением:
определена уравнением:
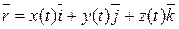 .
.
Тогда вектор:
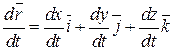 является касательным к линии
является касательным к линии 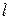 .
.
Если 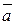 параллельно
параллельно 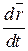 , то получим дифференциальное уравнение линии:
, то получим дифференциальное уравнение линии:
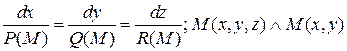 .
.
Векторное поле не только порождает семейство векторных линий, но и определяет на этих линиях направление.
Положительное направление вектора 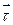 выбирается в соответствии с положительным направлением обхода кривой
выбирается в соответствии с положительным направлением обхода кривой 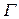 .
.
Пусть 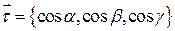 .
. 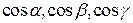 - направляющие косинусы.
- направляющие косинусы. 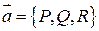 - векторное поле в прямоугольной декартовой системе координат.
- векторное поле в прямоугольной декартовой системе координат.
Тогда запись эквивалентная (1) имеет вид:
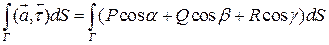 (2)
(2)
Отметим, что 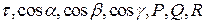 - функции параметра кривой
- функции параметра кривой  . Рассмотрим:
. Рассмотрим:
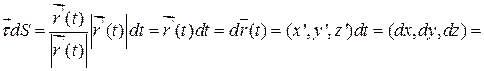
= 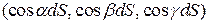 . Где
. Где 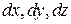 - проекции вектора
- проекции вектора 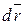 на оси координат, то интеграл можно записать в виде:
на оси координат, то интеграл можно записать в виде:
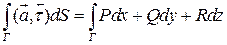 (3)
(3)
Последний интеграл (3) называют общим криволинейным интегралом II-го рода.
Его можно рассматривать как сумму трех интегралов:
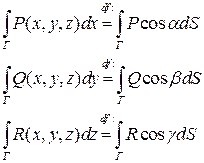 (4)
(4)
Интегралы (4) также называют криволинейными интегралами II-го рода в отличие от криволинейных интегралов I-го рода.
Формула (3) дает практически связь криволинейного интеграла II-го рода с криволинейным интегралом I-го рода.
Df.3 Пусть  - кусочно-гладкая кривая;
- кусочно-гладкая кривая;  определена на
определена на 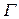 . Криволинейным от векторной функции
. Криволинейным от векторной функции 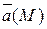 называется:
называется:
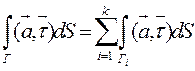 .
.
Перейдем к условиям существования криволинейного интеграла от векторной функции, т.к. он сводится (также как и криволинейный интеграл II-го рода) к криволинейному интегралу I-го рода, то эти условия имеют аналогичный вид сформулированный ранее.
Th.1 (НЕОБХОДИМОЕ УСЛОВИЕ).
Пусть существует 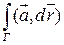 и
и 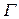 кусочно-гладкая
кусочно-гладкая 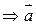 - ограничена на
- ограничена на 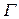 (т.е.
(т.е. 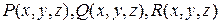 ограничены на
ограничены на 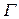 ).
).
(Б/Д).
Th.2 Пусть 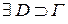 , что
, что 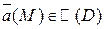 (т.е.
(т.е. 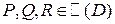 ),
), 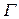 кусочно-гладкая
кусочно-гладкая 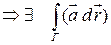 .
.
Th.3 (СВЕДЕНИЕ КРАТНОГО ИНТЕГРАЛА II-ГО РОДА К ОПРЕДЕЛЕННОМУ).
Пусть 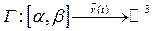 гладкая,
гладкая, 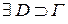 , что
, что 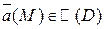 , тогда:
, тогда:
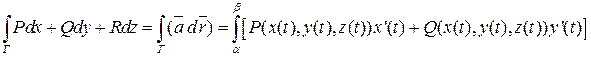 +
+
+ 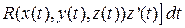 .
.
Доказательство:
По введенным определениям:
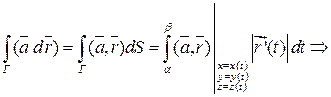
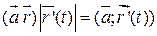 , таким образом:
, таким образом:
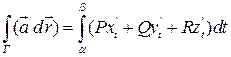 (6)
(6)
Существование интеграла следует из достаточных условий теоремы 2.
ЗАМЕЧАНИЕ.
Для плоского векторного поля 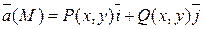 линейный интеграл
линейный интеграл 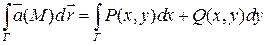 .
.
Основное правило вычисления кратного интеграла сводится к следующему: чтобы вычислить кратный интеграл вдоль данной линии, его нужно преобразовать в определенный интеграл. Для этого все переменные под знаком интеграла следует выразить через одну переменную, используя уравнения той линии, вдоль которой ведется интегрирование.
Рассмотрим плоское поле 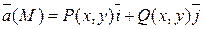 .
.
а) Если 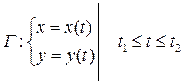
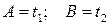 .
.
 ●
● 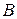
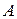 ●
●
То: 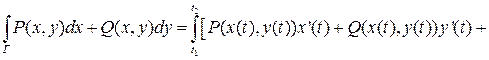
+ 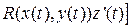
 .
.
б) Если 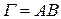 - гладкая, уравнение дуги имеет вид
- гладкая, уравнение дуги имеет вид 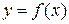 , то принимая x за параметр, получим:
, то принимая x за параметр, получим:
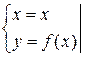 ,
,
тогда:
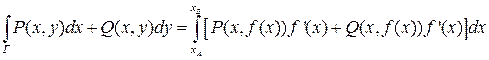 .
.
б’) Если 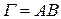 гладкая, имеет вид
гладкая, имеет вид 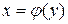 , y изменяется на
, y изменяется на 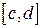 .
.
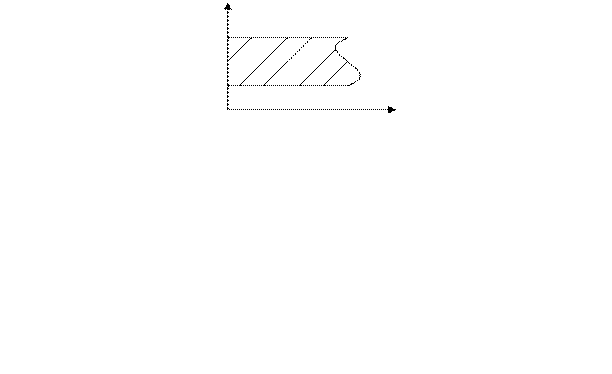
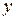
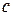
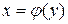
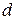
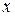
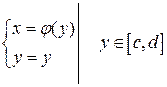 , y – параметр.
, y – параметр.
Тогда:
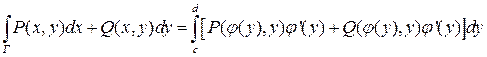 .
.
в) Если 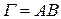 гладкая заданная системой уравнений:
гладкая заданная системой уравнений:
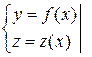 т.е. определена, как пересечение двух цилиндрических поверхностей.
т.е. определена, как пересечение двух цилиндрических поверхностей.
Тогда:
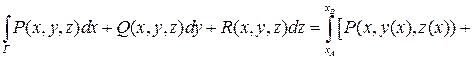
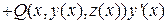 +
+ 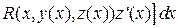 .
.
г) Если уравнение имеет более сложный вид:
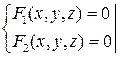 ,
,
то нужно заменить эту систему равносильной ей системой вида:
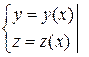 ,
,
либо введя параметр 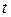 , привести к виду:
, привести к виду:
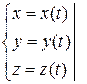 .
.
Все указанные выше формулы верны в тех случаях, когда линия 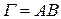 является гладкой. Если дуга
является гладкой. Если дуга 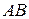 - кусочно-гладкая или состоит из различных дуг (с различными уравнениями), то криволинейный интеграл по всему пути
- кусочно-гладкая или состоит из различных дуг (с различными уравнениями), то криволинейный интеграл по всему пути 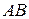 равен сумме интегралов по составляющим его дугам.
равен сумме интегралов по составляющим его дугам.
ЗАМЕЧАНИЕ 1.
Сопоставляя определение криволинейного интеграла II-го рода с определением криволинейного интеграла I-го рода, при очевидном сходстве оба определения имеют существенное различие:
1) в случае интеграла I-го рода при составлении интегральной суммы значение функции 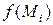 умножается на длину
умножается на длину 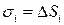 участка кривой
участка кривой 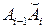 .
.
2) А в случае интеграла II-го рода это значение 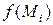 умножается на проекцию
умножается на проекцию 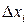 (или
(или 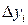 ) участка кривой
) участка кривой 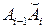 на ось x (или на ось y).
на ось x (или на ось y).
ЗАМЕЧАНИЕ 2.
а) Общий криволинейный интеграл II-го рода 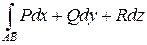 физически представляет собой работу по перемещению материальной точки из A в В вдоль кривой Г под действием силы, имеющей составляющие
физически представляет собой работу по перемещению материальной точки из A в В вдоль кривой Г под действием силы, имеющей составляющие 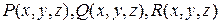 .
.
б) Физически криволинейный интеграл I-го рода 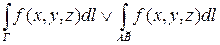 представляет собой массу кривой Г, линейная плотность вдоль которой равна
представляет собой массу кривой Г, линейная плотность вдоль которой равна 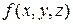 .
.
ЗАМЕЧАНИЕ 3.
Из определения криволинейных интегралов следует, что:
а) Криволинейный интеграл I-го рода не зависит от того, в каком направлении (от А к В или от В к А) пробегает кривая Г.
б) Для кратного интеграла II-го рода изменение направления на кривой ведет к изменению знака, т.е.:
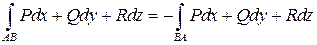 .
.
 2015-08-21
2015-08-21 842
842







