Побудова точкового графіка заданої функції

P	C
	141,1
	111,7
	86,1
	58,4
	29,1
	9,65

Табл. 1.2

Для заданої таблично функції будуємо графік, використовуючи середовище програми MS Exel.

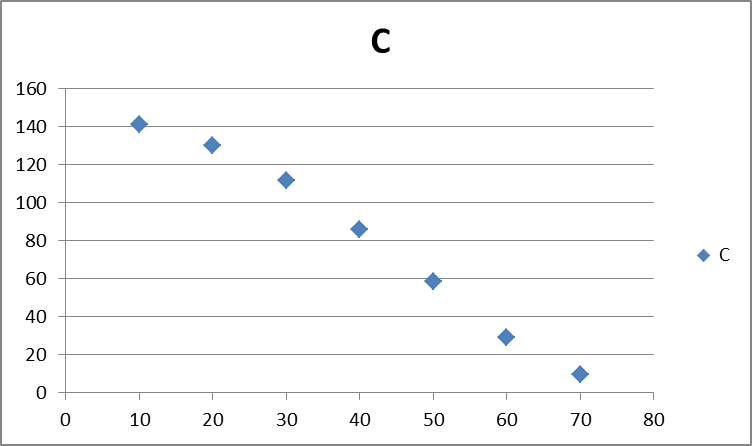
Рис.1.1 Графік заданої функції

Використовуючи графік, можна прослідкувати залежність х від у: більшому значенню х відповідає менше значення у. Отже, функція спадаюча.

1.2. Апроксимація функції поліномом першого порядку.

Обчислимо коефіцієнти системи:

№	x	y	x2	xy
		141,1
		111,7
		86,1
		58,4
		29,1
		9,56		669,2
		565,96		16141,2

Запишемо систему рівнянь:

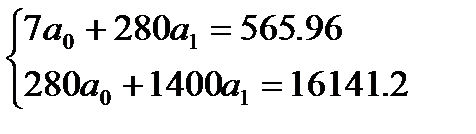
Розв’яжемо систему за схемою єдиного ділення:

хід	x1	x2	b	сума
прямий			565,96	852,96
		16141,2	30421,2
		80,85143	121,8514
		-6497,2	-3697,2
		-2,32043	-1,32043
зворотній			-2,32043	-1,32043
		173,6686	174,6686

Розв’завши цю систему маємо:

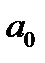=173,6686, 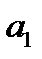=-2,32043

У=173,6686-2,32043х (1.8)

1.3. Апроксимація функції поліномом другого порядку.

Обчислимо коефіцієнти системи (1.6):

№	x	y	x2	x3	x4	xy	x2y
		141,1
		111,7
		86,1
		58,4
		29,1
		9,56				669,2
сума		565,96				16141,2

Запишемо систему рівнянь:

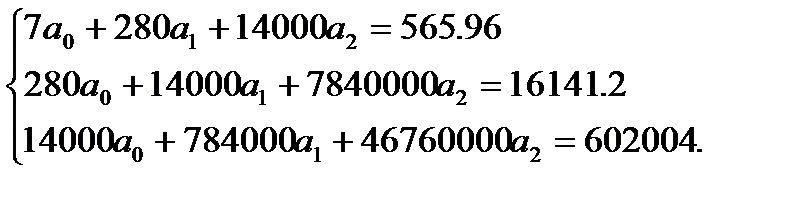
Розв’яжемо систему за схемою єдиного ділення:

хід	етапи	коефіцієнти		b	суми
		x1	x2	x3
прямий					565,96	14852,96	14853,96
					16141,2	814421,2	814421,2
					80,85143	2121,851	2121,851
					-6497,2	220302,8	220302,8
					-529916
					-2,32043	78,67957	78,67957
					-10140
					-0,01207	0,987929	0,987929
зворотній					-0,01207	0,987929	0,987929
					-1,35471	-0,35471	-0,35471
					159,1829	160,1829	160,1829

Табл. 1.5

Значення 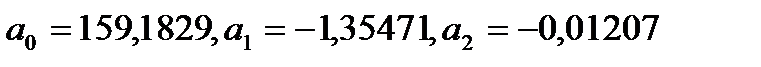підставимо у рівняння (1.5):

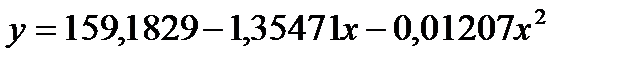. (1.9)

1.4. Оцінка точності апроксимації:

2 Порівняємо табличні значення 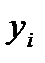з відповідними значеннями 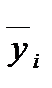, обчисленими за формулою (1.8).

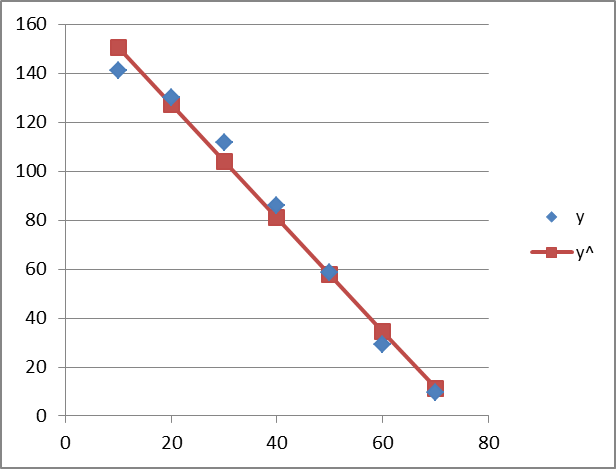
x	y	y^
	141,1	150,4643
		127,26
	111,7	104,0557
	86,1	80,85143
	58,4	57,64714
	29,1	34,44286
	9,56	11,23857

Табл. 1.6

Як видно з табл. 1.6, багаточлен (1.8) дає близьке наближення дослідних даних.

Порівняємо вихідні значення 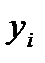з відповідними значеннями 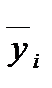, отриманих з наближеної формули (1.9). Результати наведено в табл. 1.7.

x	y	y^	(y-y^)2
	141,1	144,4286	11,07939
		127,26	7,5076
	111,7	107,6771	16,18338
	86,1	85,68	0,1764
	58,4	61,26857	8,228702
	29,1	34,44286	28,54612
	9,56	5,202857	18,98469

1.4.1.Розрахуємо середню квадратичну похибку за формулами (1.3)

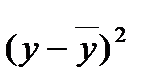
	87,68985
	7,5076
	58,4351
	27,5475
	0,566794
	28,54612
	2,817602
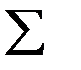
	213,1106

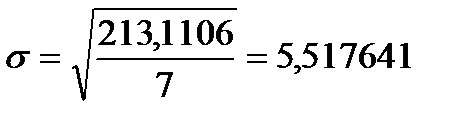
	(y-y^)2
	11,07939
	7,5076
	16,18338
	0,1764
	8,228702
	28,54612
	18,98469
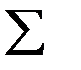
	90,70629

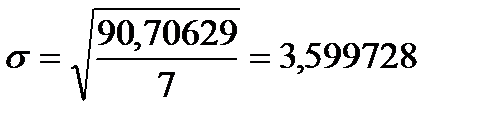
1.4.2.Графіки апроксимованих функцій

Графік апроксимованого багаточлена першого порядку

:

Графік апроксимованого багаточлена другого порядку

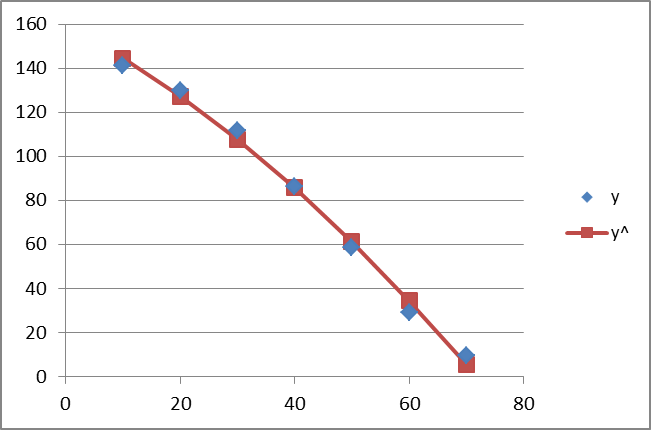
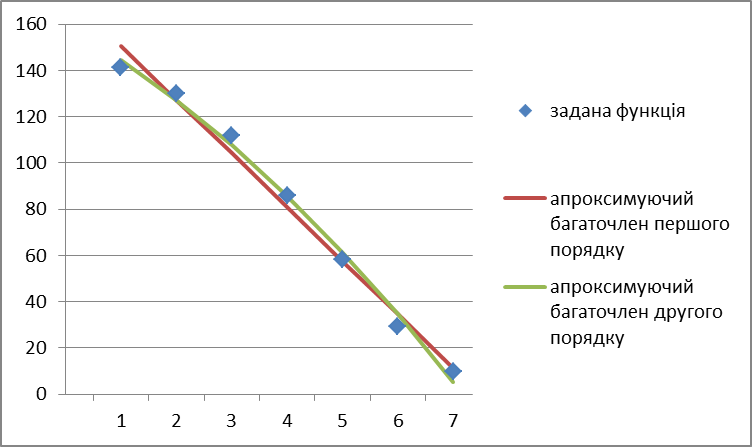
Рис. 1.2. Графік апроксимуючих функцій

1.5. Висновок: Для даної функції визначення вигляду функції апроксимацією функції поліномом другого порядку є більш точним, ніж апроксимація функції поліномом першого порядку.