Теоретичні відомості
Статистична залежність називається кореляційною, якщо у разі зміни однієї величини, змінюється середнє значення іншої.
1. Лінійна кореляція
Якщо обидві лінії регресії Y на X і X на Y – прямі, то кореляцію називають лінійною. Вибіркове рівняння прямої лінії регресії Y на X має вигляд
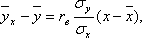
де 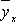 – умовна середня;
– умовна середня;
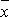 і
і 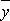 – вибіркові середні ознак X і Y;
– вибіркові середні ознак X і Y;
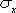 і
і 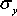 – вибіркові середні квадратичні відхилення X і Y;
– вибіркові середні квадратичні відхилення X і Y;
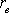 – вибірковий коефіцієнт кореляції, причому
– вибірковий коефіцієнт кореляції, причому
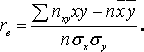
Вибіркове рівняння прямої лінії регресії X на Y має вигляд
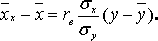
Якщо дані спостережень над ознаками X і Y задані у виді кореляційної таблиці з рівновіддаленими варіантами, то доцільно перейти до умовних варіант:
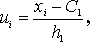
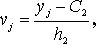
де 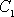 – «хибний нуль» варіант X (новий початок відліку); як хибний нуль вигідно прийняти варіанту, що розташована приблизно в середині варіаційного ряду (умовимося приймати як хибний нуль варіанту, що має найбільшу частоту);
– «хибний нуль» варіант X (новий початок відліку); як хибний нуль вигідно прийняти варіанту, що розташована приблизно в середині варіаційного ряду (умовимося приймати як хибний нуль варіанту, що має найбільшу частоту);
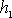 – крок, тобто різниця між двома сусідніми варіантами X;
– крок, тобто різниця між двома сусідніми варіантами X;
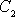 – «хибний нуль» варіант Y (новий початок відліку);
– «хибний нуль» варіант Y (новий початок відліку);
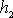 – крок, тобто різниця між двома сусідніми варіантами Y.
– крок, тобто різниця між двома сусідніми варіантами Y.
У цьому випадку вибірковий коефіцієнт кореляції
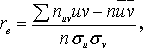
Величини 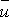 ,
, 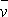 ,
, 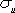 ,
, 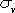 можуть бути знайдені або методом добутків (при великому числі даних), або безпосередньо за формулами:
можуть бути знайдені або методом добутків (при великому числі даних), або безпосередньо за формулами:
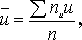
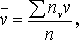
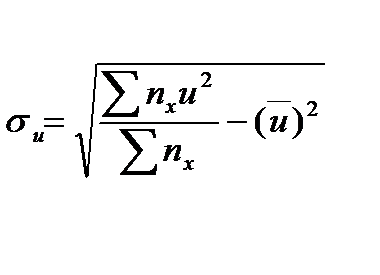
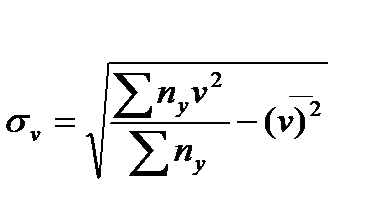
Знаючи ці величини, можна обчислити величини, що входять в рівняння регресії за формулами:
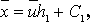
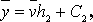
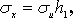
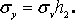
Для оцінки сили лінійного кореляційного зв'язку служить вибірковий коефіцієнт кореляції 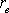 .
.
Для обґрунтованого судження про наявність зв'язку між кількісними ознаками варто перевірити, чи значимий вибірковий коефіцієнт кореляції.
Кореляційну залежність у від х можна визначити як функціональну залежність умовної середньої у від х. Виконавши певні алгебраїчні перетворення отримаємо:
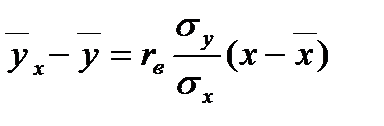 (3.1) – рівняння регресії у на х;
(3.1) – рівняння регресії у на х;
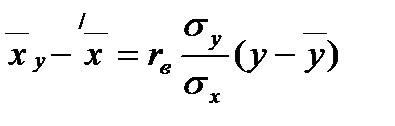 (3.2) - рівняння регресії х на у.
(3.2) - рівняння регресії х на у.
Функцію f(x) (або f(y)) називають регресією у на х (або х на у). Графік цієї функції називається лінією регресії.
Тіснота зв’язку між х та у оцінюється за допомогою коефіцієнта кореляції 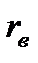 . Для незалежних величин
. Для незалежних величин 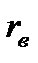 =0. Такі величини називаються некорельованими, а корельованими є ті величини, у яких коефіцієнт кореляції відповідно відмінний від нуля. Якщо |
=0. Такі величини називаються некорельованими, а корельованими є ті величини, у яких коефіцієнт кореляції відповідно відмінний від нуля. Якщо | 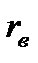 |> 0,75, це свідчить про наявність зв’язку між величинами. Якщо |
|> 0,75, це свідчить про наявність зв’язку між величинами. Якщо | 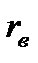 | > 0,997, то зв'язок між величинами дуже тісний. Кореляційний коефіцієнт не може перевищувати 1.
| > 0,997, то зв'язок між величинами дуже тісний. Кореляційний коефіцієнт не може перевищувати 1.
3.1. Рівняння прямих ліній регресії X на Y, Y на X;
| 1-9 | 9-17 | 17-25 | 25-33 | 33-41 | 41-49 | ny | y | V | nyV | nyV2 | q | qV | |
| 13-23 | -2 | -24 | -23 | ||||||||||
| 23-33 | -1 | -14 | -13 | ||||||||||
| 33-43 | 25,5 | ||||||||||||
| 43-53 | |||||||||||||
| 53-63 | |||||||||||||
| nx | -6 | ||||||||||||
| x | |||||||||||||
| U | -2,5 | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | |||||||
| nxU | -12,5 | -19,5 | -9 | 26,5 | 5,5 | ||||||||
| nxU2 | 31,25 | 29,25 | 4,5 | 13,25 | 22,5 | 12,5 | 113,25 | ||||||
| t | -10 | -20 | -2 | ||||||||||
| tU |
Табл. 3.1.
Результати обчислень будемо записувати до кореляційної таблиці (табл. 3.1). Перейдемо від початкових варіант 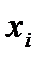 та
та 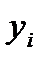 до умовних варіант:
до умовних варіант:
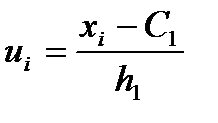 і
і 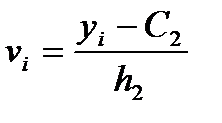 ,
,
де 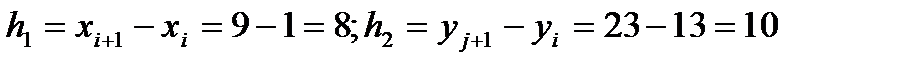 . Як
. Як 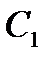 візьмемо варіанту х =29, що має найбільшу частоту
візьмемо варіанту х =29, що має найбільшу частоту 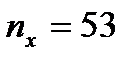 , як
, як 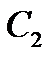 - варіанту у =38, що має найбільшу частоту
- варіанту у =38, що має найбільшу частоту 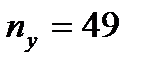 .
.
Елементи рядка 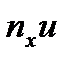 дорівнюють добуткам відповідних елементів рядків
дорівнюють добуткам відповідних елементів рядків 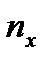 і u; елементи стовпця
і u; елементи стовпця 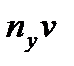 дорівнюють добуткам відповідних елементів стовпця
дорівнюють добуткам відповідних елементів стовпця 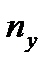 і v; аналогічно заповнюємо рядок
і v; аналогічно заповнюємо рядок 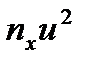 і стовпець
і стовпець 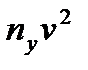 .
.
Кожен елемент стовпця q дорівнює сумі добутків частот 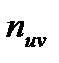 , які знаходяться у відповідному рядку вихідної кореляційної таблиці, на відповідні елементи рядка u:
, які знаходяться у відповідному рядку вихідної кореляційної таблиці, на відповідні елементи рядка u:
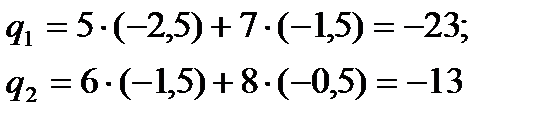
У рядку t кожен елемент дорівнює сумі добутків частот 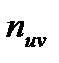 , які знаходяться у відповідному стовпці кореляційної таблиці, на відповідні елементи стовпця v:
, які знаходяться у відповідному стовпці кореляційної таблиці, на відповідні елементи стовпця v:
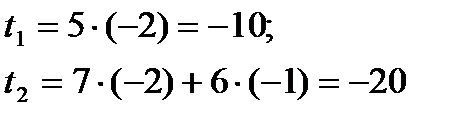 і т.д.
і т.д.
У стовпці qv кожен елемент дорівнює добутку відповідних елементів і стовбців q і v, в останньому ряду кожен елемент дорівнює добутку відповідних елементів t і u. Рівність сум  використовується для контролю правильності обчислень.
використовується для контролю правильності обчислень.
Далі знаходимо:
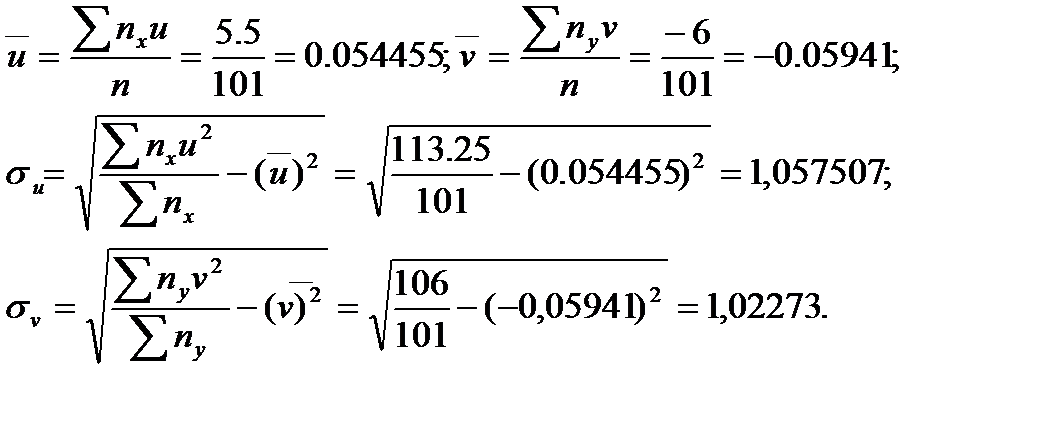
Тепер знайдемо:
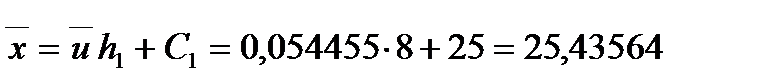 ;
;
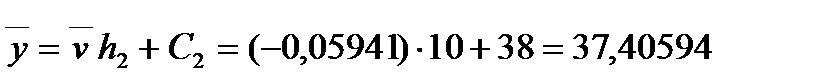 ;
;
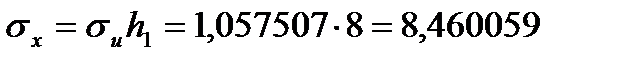 ;
;
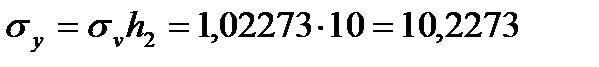 .
.
Підставивши знайдені величини в (3.1), отримаємо шукане рівняння:
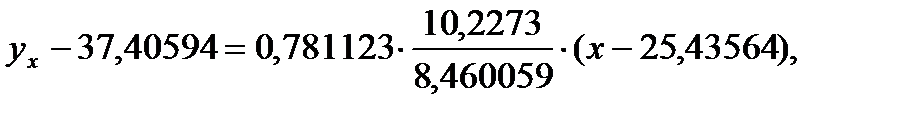
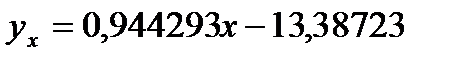 - рівняння регресії у на х;
- рівняння регресії у на х;
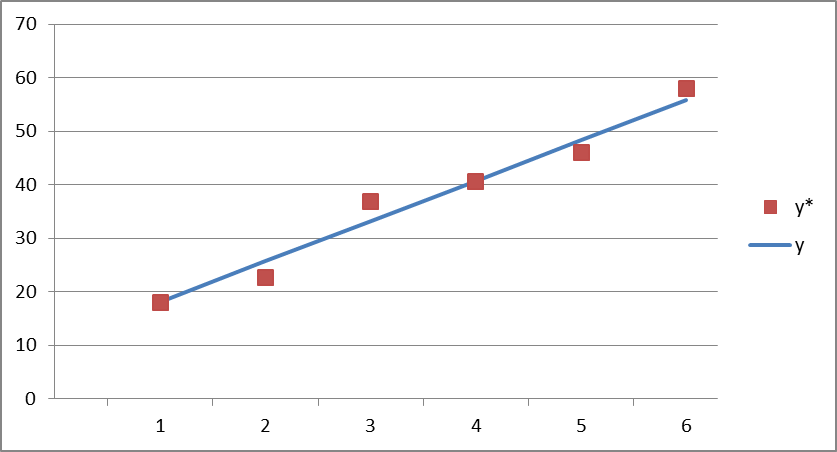
Порівняємо у з рівняння регресії і у, підрахований за таблицею:
| x | yx | yx*табл |
| 18,1087 | ||
| 25,66304 | 22,61538 | |
| 33,21739 | 36,88889 | |
| 40,77174 | 40,64151 | |
| 48,32609 | ||
| 55,88043 |
Підставивши знайдені величини в (3.1), отримаємо шукане рівняння:
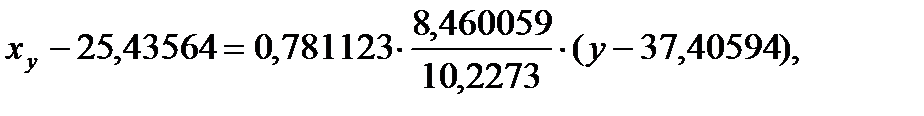
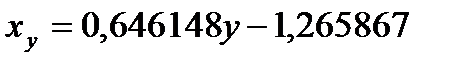 рівняння регресії х на у.
рівняння регресії х на у.
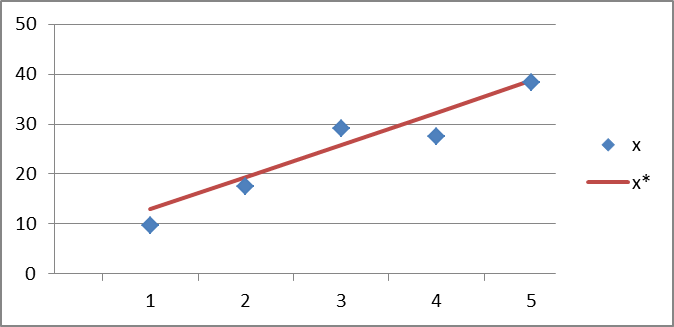
Порівняємо х з рівняння регресії і х*, підрахований за таблицею:
| YI | ẍy | ẍy* |
| 9,666667 | 12,89653 | |
| 17,57143 | 19,35801 | |
| 29,16327 | 25,81949 | |
| 27,4 | 32,28097 | |
| 38,33333 | 38,74246 |
3.2. Знайдемо коефіцієнт кореляції:
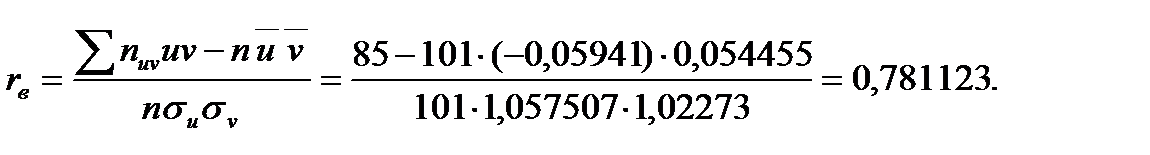
Зв'язок між величинами наявний, але він не дуже тісний.
3.3.Висновок: в даній роботі ми знаходили рівняння прямих ліній регресії X на Y, Y на X, розрахували вибірковий коефіцієнт кореляції та оцінили силу зв’язку Y і X
.
Додаток 1
| поліном першого порядку | |||||||||
| № | x | y | x2 | xy | y^ | (y-y^)2 | |||
| 141,1 | =B26^2 | =B26*C26 | =$E$40+$F$40*B26 | =(C26-F26)^2 | |||||
| =B27^2 | =B27*C27 | =$E$40+$F$40*B27 | =(C27-F27)^2 | ||||||
| 111,7 | =B28^2 | =B28*C28 | =$E$40+$F$40*B28 | =(C28-F28)^2 | |||||
| 86,1 | =B29^2 | =B29*C29 | =$E$40+$F$40*B29 | =(C29-F29)^2 | |||||
| 58,4 | =B30^2 | =B30*C30 | =$E$40+$F$40*B30 | =(C30-F30)^2 | |||||
| 29,1 | =B31^2 | =B31*C31 | =$E$40+$F$40*B31 | =(C31-F31)^2 | |||||
| 9,56 | =B32^2 | =B32*C32 | =$E$40+$F$40*B32 | =(C32-F32)^2 | |||||
| сума | =СУММ(B26:B34) | =СУММ(C26:C34) | =СУММ(D26:D34) | =СУММ(E26:E34) | =СУММ(G26:G34) | ||||
| =A32 | =B33 | =C33 | a0 | a1 | |
| =B33 | =D33 | =E33 | =C50 | =C49 |
| середня кв. похибка |
| =КОРЕНЬ(G33/A32) |
| схема єдиного ділення | ||||
| x1 | x2 | b | сума | |
| =A39 | =B39 | =C39 | =A44+B44+C44 | |
| =A40 | =B40 | =C40 | =A45+B45+C45 | |
| =A44/A44 | =B44/A44 | =C44/A44 | =D44/A44 | |
| =B45-A45*B46 | =C45-A45*C46 | =B47+C47 | ||
| =B47/B47 | =C47/B47 | =B48+C48 | ||
| =C48 | =D48 | |||
| =C46-B46*C49 | =D46-B46*D49 | |||
| поліном другого порядку | |||||||||
| № | x | y | x2 | x3 | x4 | xy | x2y | ||
| =B26 | =C26 | =B56^2 | =B56^3 | =B56^4 | =B56*C56 | =D56*C56 | |||
| =B27 | =C27 | =B57^2 | =B57^3 | =B57^4 | =B57*C57 | =D57*C57 | |||
| =B28 | =C28 | =B58^2 | =B58^3 | =B58^4 | =B58*C58 | =D58*C58 | |||
| =B29 | =C29 | =B59^2 | =B59^3 | =B59^4 | =B59*C59 | =D59*C59 | |||
| =B30 | =C30 | =B60^2 | =B60^3 | =B60^4 | =B60*C60 | =D60*C60 | |||
| =B31 | =C31 | =B61^2 | =B61^3 | =B61^4 | =B61*C61 | =D61*C61 | |||
| =B32 | =C32 | =B62^2 | =B62^3 | =B62^4 | =B62*C62 | =D62*C62 | |||
| сума | =СУММ(B56:B62) | =СУММ(C56:C62) | =СУММ(D56:D62) | =СУММ(E56:E62) | =СУММ(F56:F62) | =СУММ(G56:G62) | =СУММ(H56:H62) | ||
| y^ | (y-y^)2 | ||||||||
| =$F$68+$G$68*B56+$H$68*(B56^2) | =(C56-I56)^2 | ||||||||
| =$F$68+$G$68*B57+$H$68*(B57^2) | =(C57-I57)^2 | ||||||||
| =$F$68+$G$68*B58+$H$68*(B58^2) | =(C58-I58)^2 | ||||||||
| =$F$68+$G$68*B59+$H$68*(B59^2) | =(C59-I59)^2 | ||||||||
| =$F$68+$G$68*B60+$H$68*(B60^2) | =(C60-I60)^2 | ||||||||
| =$F$68+$G$68*B61+$H$68*(B61^2) | =(C61-I61)^2 | ||||||||
| =$F$68+$G$68*B62+$H$68*(B62^2) | =(C62-I62)^2 | ||||||||
| =СУММ(J56:J62) | |||||||||
| коефіцієнти | |||||||
| =A62 | =B63 | =D63 | =C63 | ||||
| =B63 | =D63 | =E63 | =G63 | a0 | a1 | a2 | |
| =D63 | =E63 | =F63 | =H63 | =F87 | =F86 | =F85 |
| середня кв. похибка | |
| =КОРЕНЬ(J63/A62) |
схема єдиного ділення
| хід | етапи | коефіцієнти | b | суми | |||
| x1 | x2 | x3 | |||||
| прямий | =A68 | =B68 | =C68 | =D68 | =C76+D76+E76+F76 | =B76+C76+D76+E76+F76 | |
| =A69 | =B69 | =C69 | =D69 | =C77+D77+E77+F77 | =C77+D77+E77+F77 | ||
| =A70 | =B70 | =C70 | =D70 | =C78+D78+E78+F78 | =C78+D78+E78+F78 | ||
| =C76/C76 | =D76/C76 | =E76/C76 | =F76/C76 | =G76/C76 | =C79+D79+E79+F79 | ||
| =D77-C77*D79 | =E77-C77*E79 | =F77-C77*F79 | =D80+E80+F80 | =D80+E80+F80 | |||
| =D78-C78*D79 | =E78-C78*E79 | =F78-C78*F79 | =D81+E81+F81 | =D81+E81+F81 | |||
| =D80/D80 | =E80/D80 | =F80/D80 | =G80/D80 | =D82+E82+F82 | |||
| =E81-D81*E82 | =F81-D81*F82 | =E83+F83 | =E83+F83 | ||||
| =E83/E83 | =F83/E83 | =G83/E83 | =E84+F84 | ||||
| зворотній | =F84 | =G84 | =E85+F85 | ||||
| =F82-E82*F85 | =G82-E82*G85 | =D86+F86 | |||||
| =F79-E79*F85-D79*F86 | =G79-E79*G85-D79*G86 | =C87+F87 |
Додаток 2
| 2.1) | |||||
| xi | |||||
| ni | |||||
| N | =B3+C3+D3+E3+F3 | ||||
| x ≤2 | |||||
| 2<x ≤5 | =B3/B4 | ||||
| 5<x ≤7 | =(B3+C3)/B4 | ||||
| 7<x ≤11 | =(B3+C3+D3)/B4 | ||||
| 11<x ≤15 | =(B3+C3+D3+E3)/B4 | ||||
| x >15 | =(B3+C3+D3+E3+F3)/B4 |
| 2.2) | |||||
| Ii | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 |
| ni | |||||
| ni/h | =B16/H15 | =C16/H15 | =D16/H15 | =E16/H15 | =F16/H15 |
| Wi | =B16/H16 | =C16/H16 | =D16/H16 | =E16/H16 | =F16/H16 |
| Wi/h | =B19/H15 | =C19/H15 | =D19/H15 | =E19/H15 | =F19/H15 |
| Ii | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 |
| ni | |||||
| xi | =(2+5)/2 | =(5+8)/2 | =(8+11)/2 | =(11+14)/2 | =(14+17)/2 |
| N | =B23+C23+D23+E23+F23 |
| xв | =(B23*B24+C23*C24+D23*D24+E23*E24+F23*F24)/I24 |
| DB | =((B23*(B24-I25)^2)+(C23*(C24-I25)^2)+(D23*(D24-I25)^2)+(E23*(E24-I25)^2)+(F23*(F24-I25)^2))/I24 |
| σB | =КОРЕНЬ(I26) |
| xr | =I25 |
| D | =(I26/(I24-1))*I24 |
| σr | =КОРЕНЬ(I29) |
Додаток 3
| Ū | =I14/I11 | |||||
| Ṽ | =L11/I11 | |||||
| Ϭu | =КОРЕНЬ((I15/I11)-(C19^2)) | |||||
| Ϭv | =КОРЕНЬ((M11/I11)-(C20^2)) | |||||
| rв | =(I17-(I11*C19*C20))/(I11*C21*C22) | |||||
| ẍ | =(C19*8)+R10 | |||||
| ȳ | =(C20*10)+J8 | |||||
| Ϭx | =C21*8 | |||||
| Ϭy | =C22*10 | |||||
| Y | =(C23*C27)/C26 | =((C23*C27)/C26)*(-C24)+C25 | ȳx=0,944293x+13038723 | |||
| XI | ȳx | ȳx* | ȳx*-ȳx | |||
| =C5 | =(C6*B6)/C11 | =$C$26*B32+$D$26 | =D32-C32 | |||
| =D5 | =(D6*B6+D7*B7)/D11 | =$C$26*B33+$D$26 | =D33-C33 | |||
| =E5 | =(E7*B7+E8*B8+E9*B9)/E11 | =$C$26*B34+$D$26 | =D34-C34 | |||
| =F5 | =(F8*B8+F9*B9+F10*B10)/F11 | =$C$26*B35+$D$26 | =D35-C35 | |||
| =G5 | =(G8*B8+G9*B9+G10*B10)/G11 | =C29*B36+D29 | =D36-C36 | |||
| =H5 | =(H10*B10)/H11 | =C29*B37+D29 | =D37-C37 |
 2015-08-12
2015-08-12 870
870







