Теоретичні відомості
2.1.Емпірична функція статистичного розподілу.


Висновок 1. Імовірність того, що випадкова величина X набуде значення, яке знаходиться в інтервалі (а, b), дорівнює приросту функції розподілу на цьому інтервалі:
Р(а < х < b) = F(b) - F(a).
Висновок 2. Імовірність того, що неперервна, випадкова величина X набуде одного визначеного значення, наприклад хь дорівнює нулеві:
Р(Х = х 0 = 0.
3. Якщо всі можливі значення випадкової величини X належать інтервалові (а, b), то F(x) = 0 при х <а, F(x) = 1 при х > b.
Висновок. Якщо можливі значення неперервної випадкової величини розташовані на всій осі Ох, то слушні такі граничні співвідношення:
lim F{x)- 0; lim F(x) = l.
Емпіричною (або статистичною) функцією розподілу випадкової величини ξ називається частота події, що полягає в тому, що величина ξ в результаті випробовування прийме значення, менше х:
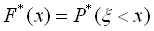
На практиці достатньо знайти значення статистичної функції розподілу в точках х0, х1, …, хk, що є кінцями інтервалів статистичного ряду:
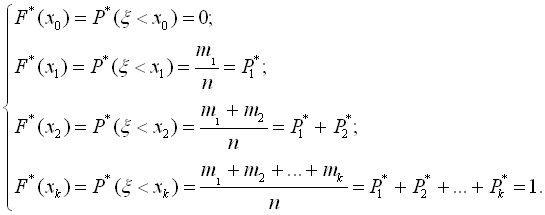
Гістограмою частот називають східчасту фігуру, що складається що складається з прямокутників, основами яких є значення кроку h, а висотами – густина частоти 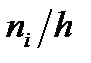 (
(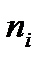 - сума частот варіант, що потрапили в і -й інтервал).
- сума частот варіант, що потрапили в і -й інтервал).
Площа гістограми частот дорівнює об’єму вибірки N.
Гістограмою відносних частот називають східчасту фігуру, що складається з прямокутників, основами яких є значення кроку h, а висоти дорівнюють 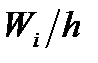 (густина відносної частоти).
(густина відносної частоти).
Площа гістограми відносних частот дорівнює 1.
Вибіркова середня – це середня зважена значень випадкової величини Х з вагами, які дорівнюють відповідним частотам:
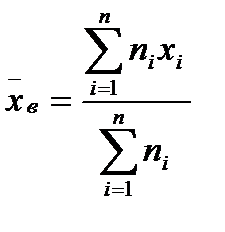 (2.1)
(2.1)
Вибіркова дисперсія – це середня зважена квадратів відхилень значень 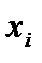 від їх середнього значення
від їх середнього значення 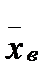 з вагами, які дорівнюють відповідним частотам:
з вагами, які дорівнюють відповідним частотам:
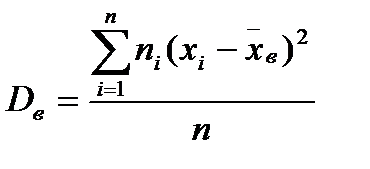
На практиці використовують більшу зручну формулу для обчислення дисперсії:
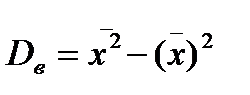 ,
,
де 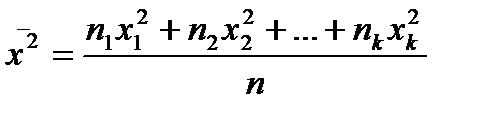 - середнє значення квадратів
- середнє значення квадратів 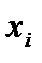 ;
; 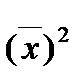 - квадрат середнього значення
- квадрат середнього значення 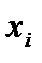 , обчисленого за формулою (2.1).
, обчисленого за формулою (2.1).
Середнім квадратичним відхиленням називають квадратний корінь із вибіркової дисперсії:
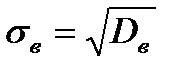
Статистичні оцінки нормального розподілу
Оцінку називають точковою, якщо вона визначається одним числом. Отже, точковою статистичною оцінкою генеральної середньої є вибіркова середня:
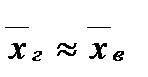
Точкова статистична оцінка генеральної дисперсії обчислюється за формулою:
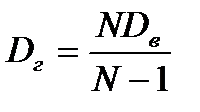
Статистична оцінка середнього квадратичного відхилення є квадратним коренем із генеральної дисперсії:
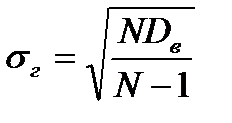
 2015-08-12
2015-08-12 379
379








