Для даної випадкової величини, заданої рядом розподілу
| xi | |||||
| ni |
об’єм вибірки дорівнює
| N |
функція розподілу має вигляд
| x ≤2 | |
| 2<x ≤5 | 0,088889 |
| 5<x ≤7 | 0,222222 |
| 7<x ≤11 | 0,333333 |
| 11<x ≤15 | 0,555556 |
| x >15 |
2.2.1. Гістограма частот та відносних частот
| Ii | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 |
| xi | 3,5 | 6,5 | 9,5 | 12,5 | 15,5 |
| ni | |||||
| ni/h | 4,666667 | 6,666667 | 8,333333 | 1,666667 | |
| Wi | 0,085714 | 0,2 | 0,285714 | 0,357143 | 0,071429 |
На осі абсцис відкладемо заданий крок довжиною h =5-2=3. Над цими інтервалами проведемо відрізки, паралельні осі абсцис, на відстані  / h, для чого знайдемо:
/ h, для чого знайдемо:
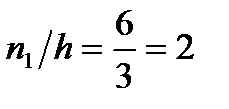 ;
; 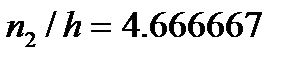 ;
; 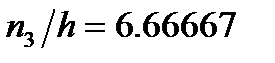 ;
; 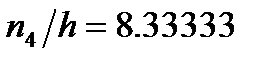 ;
; 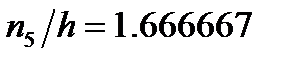 .
.
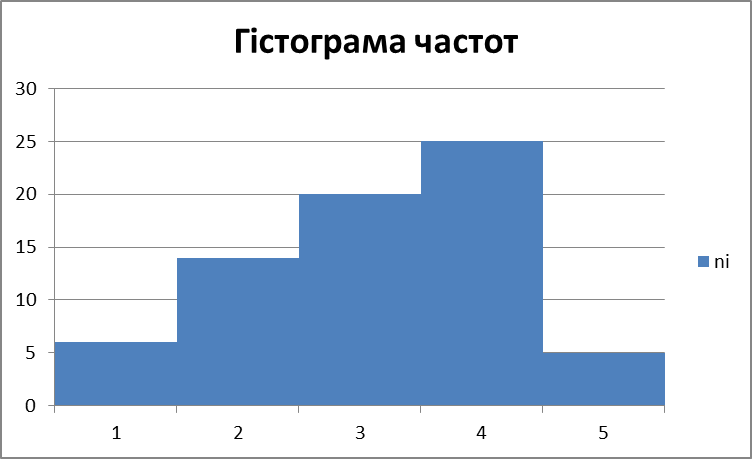
Рис. 2.1
Для побудови діаграми відносних частот знайдемо їх густини:
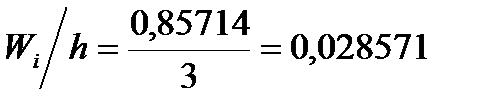 ;
; 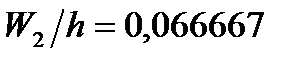 ;
; 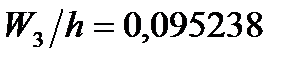 ;
; 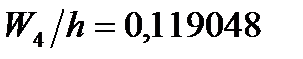 ;
; 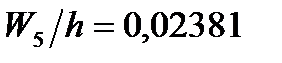
Відкладемо на осі абсцис інтервали. Проведемо над ними відрізки, паралельні осі абсцис, на відстані 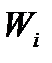 /h.
/h.
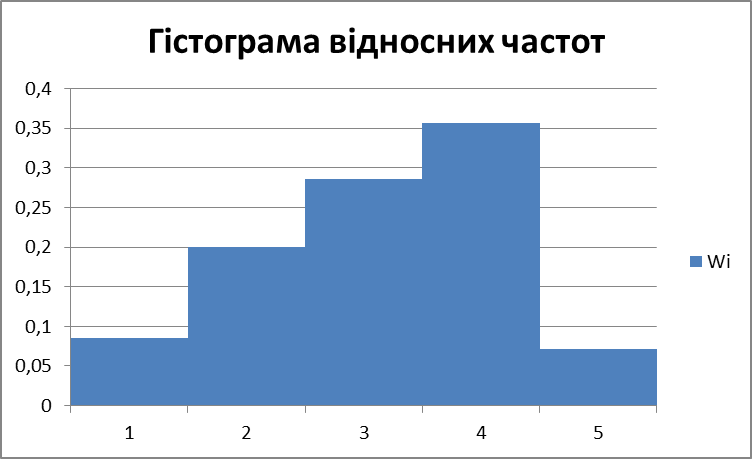
Рис. 2.2
2.2.2. Числові характеристики вибірки
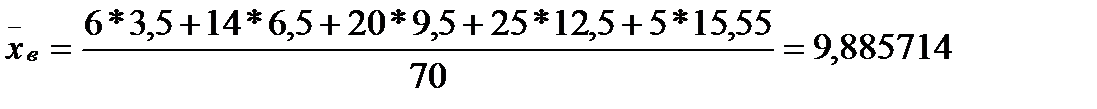 ;
;
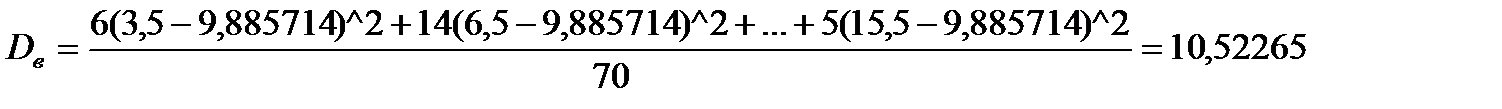 ;
;
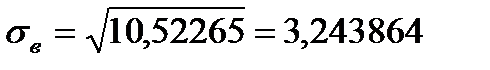 .
.
2.2.3. Статистичні оцінки генеральної середньої, дисперсії та середнього квадратичного відхилення
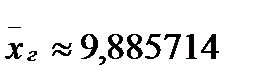
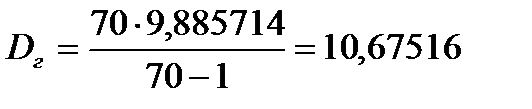 ;
;
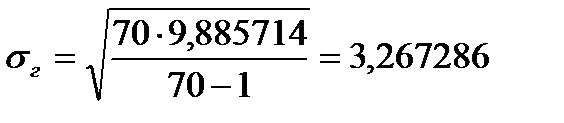 .
.
2.3.Висновок: в даній роботі ми працювали з деякими елементами статистичного розподілу, будували гістограму частот та гістограму відносних частот заданої нам вибірки, подали числові характеристики вибірки, підрахували статистичні оцінки генеральної середньої дисперсії та середнього квадратичного відхилення.
 2015-08-12
2015-08-12 431
431








