З метою спрощення математичних перетворень, розглянемо функцію двох аргументів 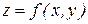 , припускаю її досить гладкої, тобто крапки, що має в достатній околиці ( x, y) безперервні похідні першого порядку. Припустимо також, що відомо абсолютні
, припускаю її досить гладкої, тобто крапки, що має в достатній околиці ( x, y) безперервні похідні першого порядку. Припустимо також, що відомо абсолютні 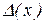 ,
, 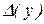 і відносні
і відносні 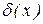 ,
, 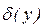 погрішності її аргументів. Поставимо задачу визначити абсолютну
погрішності її аргументів. Поставимо задачу визначити абсолютну 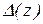 й відносну
й відносну 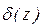 погрішності обчислення функції в крапці (x, y).
погрішності обчислення функції в крапці (x, y).
Оцінимо абсолютну величину погрішності функції. Із цією метою, використовуючи теорему Лагранжа, одержиме
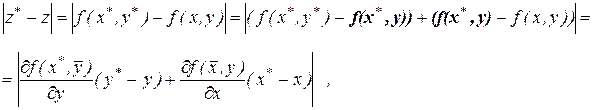 (1.9)
(1.9)
де 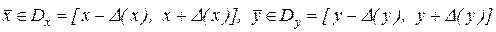 .
.
Використовуючи, далі властивість модуля суми, маємо
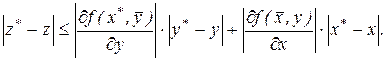 .
.
І, нарешті, крім залежності оцінки від невідомих величин 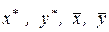 , одержиме
, одержиме
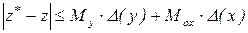 ,
,
де 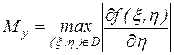 ,
, 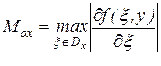 ,
,
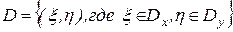 .
.
Позначимо
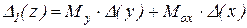 .
.
Якщо на качану перетворень (1.9) до вихідного вираження додати 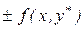 , те в результаті аналогічних дій одержимо другові оцінку
, те в результаті аналогічних дій одержимо другові оцінку
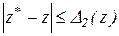 ,
,
де
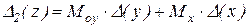 ,
,
де
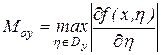 ,
, 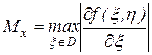 .
.
Тоді, мабуть, у якості 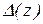 необхідно взяти найменшу з них, тобто покласти
необхідно взяти найменшу з них, тобто покласти
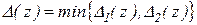 .
.
Якщо ж допустити, що цілком природно, достатню малість абсолютних погрішностей 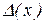
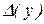 , те в якості
, те в якості 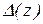 можна взяти більше просту, однак трохи завищену оцінку
можна взяти більше просту, однак трохи завищену оцінку
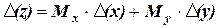 . (1.10)
. (1.10)
Дійсно, у силу 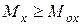 ,
, 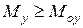 , очевидно
, очевидно 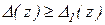 й
й 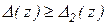 .
.
У цьому випадку з (1.10) для 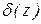 треба вираження
треба вираження
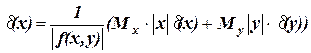 (1.11)
(1.11)
Аналогічним образом, для функції декількох змінних 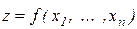 , одержиме
, одержиме
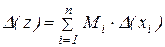
і
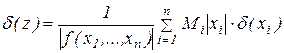 ,
,
де
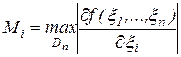 .
.
 2015-08-21
2015-08-21 305
305








