Установимо характер розвитку погрішностей при виконанні арифметичних операцій. Позначимо 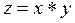 , де
, де 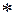 - один із символів ±, ∙, ÷. Будемо вважати відомими погрішності операндов ∆(x), ∆(y), δ(x), δ(y) і позначимо через
- один із символів ±, ∙, ÷. Будемо вважати відомими погрішності операндов ∆(x), ∆(y), δ(x), δ(y) і позначимо через 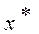 ,
, 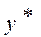 ,
, 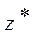 їхні точні значення.
їхні точні значення.
Додавання. У цьому випадку 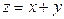 , де
, де 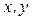 - числа одного знака. Тоді справедливі наступні оцінки
- числа одного знака. Тоді справедливі наступні оцінки
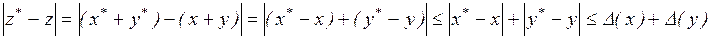 .
.
Таким чином, маємо
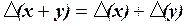 , (1.1)
, (1.1)
т.е. абсолютна погрішність суми двох наближених чисел дорівнює сумі абсолютних погрішностей доданків.
Отриманий результат очевидним образом узагальнюється й на довільне число доданків.
Далі, тому що
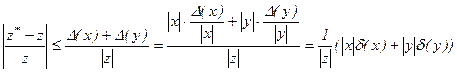 ,
,
тобто
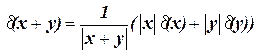 . (1.2)
. (1.2)
Вирахування. У цьому випадку 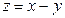 , де значення
, де значення 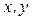 - числа одного знака. Також, як і у випадку додавання, отут
- числа одного знака. Також, як і у випадку додавання, отут
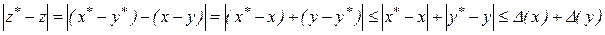
т.е.
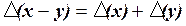 , (1.3)
, (1.3)
що збігається з (1.1).
У такий же спосіб,
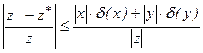 ,
,
і
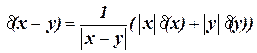 , (1.4)
, (1.4)
що збігається з (1.2).
Аналіз виражень (1.3), (1.4) показує, що при вирахуванні близьких чисел, тобто при z > 0, погрішність?(z) може перевищувати результат, а величина?(z)>?. Тому при обчисленнях необхідно уникати вирахування близьких чисел.
Множення. У цьому випадку 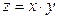 . Тоді
. Тоді
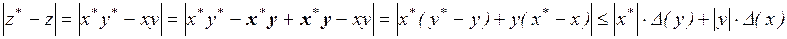
Далі, з огляду на
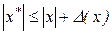 ,
,
маємо
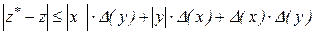 .
.
У такий спосіб
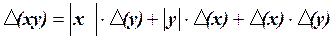 , (1.5)
, (1.5)
а
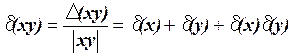 . (1.6)
. (1.6)
Відзначимо, якщо 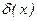 або
або 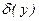 ‹‹ 1, ті
‹‹ 1, ті
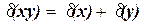 . (1.61)
. (1.61)
Ділення. У цьому випадку 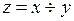 . Тоді
. Тоді
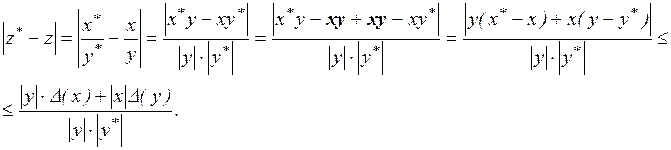
З огляду на, що 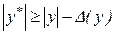 , маємо
, маємо
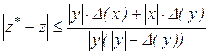 .
.
У такий спосіб
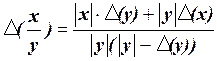 , (1.7)
, (1.7)
Отут, природно, передбачається, що 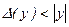 .
.
Далі, тому що
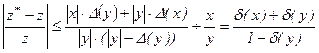 ,
,
ті
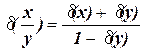 (1.8)
(1.8)
Якщо 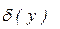 ‹‹ 1, ті
‹‹ 1, ті
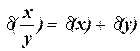 ,
,
що збігається з (1.61).
Зведемо в таблицю отримані результати.
Таблиця 1.1. Погрішності виконання арифметичних операцій
| № | Операція | 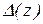
| 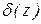
| Примітки |
| 1. | z=x+ y |
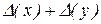
| 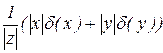
| |
| 2. | z=x - y |
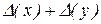
| 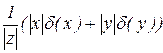
| |
| 3. | z=x y | 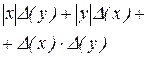
|
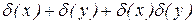
| 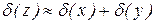 ,
якщо ,
якщо 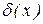 або або
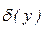 ‹‹ 1 ‹‹ 1
|
| 4. |
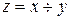
| 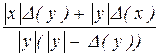
| 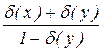
| 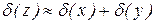 ,
якщо ,
якщо
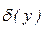 ‹‹ 1 ‹‹ 1
|
 2015-08-21
2015-08-21 309
309








