Ці поняття ставляться до числа базових у теорії погрішностей.
Позначимо через 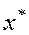 точне значення деякої величини, через x,- його наближене значення. Тоді різниця
точне значення деякої величини, через x,- його наближене значення. Тоді різниця 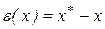 називається погрішністю наближеного числа x. При діях з наближеними числами звичайно відомо, що абсолютна величина погрішності
називається погрішністю наближеного числа x. При діях з наближеними числами звичайно відомо, що абсолютна величина погрішності 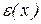 не перевершує деякої величини
не перевершує деякої величини 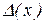 , тобто
, тобто
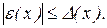
Величина 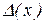 являє собою оцінку абсолютної величини погрішності й називається граничною абсолютною погрішністю наближеного числа x. Природно, у якості
являє собою оцінку абсолютної величини погрішності й називається граничною абсолютною погрішністю наближеного числа x. Природно, у якості 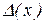 , за наявною інформацією, вибирають найменшу величину, що задовольняє зазначеній умові. Відзначимо, що при наявності
, за наявною інформацією, вибирають найменшу величину, що задовольняє зазначеній умові. Відзначимо, що при наявності 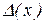 може бути встановлений і діапазон розташування точного значення x. Дійсно, тому що
може бути встановлений і діапазон розташування точного значення x. Дійсно, тому що 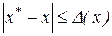 , то
, то 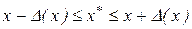 .
.
Відношення
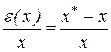
являє собою відносну погрішність наближеного числа x. Алі тому що 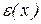 , загалом кажучи, не відома, ті в якості відносної приймають верхню оцінку
, загалом кажучи, не відома, ті в якості відносної приймають верхню оцінку 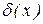 модуля цього відношення. Тобто. величина
модуля цього відношення. Тобто. величина 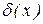 , така, що
, така, що
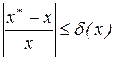
називається граничною відносною погрішністю числа x. Очевидно, що 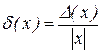 й
й 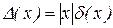 .
.
Іноді величину 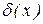 виражають і у відсотках. Помітимо, що при наявності
виражають і у відсотках. Помітимо, що при наявності 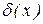 також може бути встановлений діапазон розташування точного значення. Дійсно, тому що
також може бути встановлений діапазон розташування точного значення. Дійсно, тому що
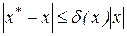 ,
,
ті 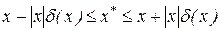 .
.
 2015-08-21
2015-08-21 384
384








