У принциповому плані він являє собою узагальнення раніше розглянутого методу дотичних.
Припустимо, що вихідна система рівнянь має вигляд (5.4) або в згорнутому вигляді
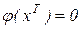 . (5.41)
. (5.41)
Нехай 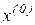 ,- деяке наближення до рішення. Розкладемо ліві частини (5.4), (5.41) по формулі Тейлора, обмежуючись обліком малих першого порядку. У результаті цього, одержимо
,- деяке наближення до рішення. Розкладемо ліві частини (5.4), (5.41) по формулі Тейлора, обмежуючись обліком малих першого порядку. У результаті цього, одержимо
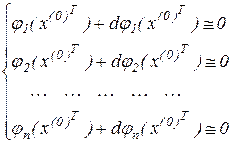 ,
,
або, у більше зручному, матричному вигляді
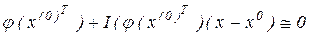 ,
,
де 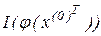 ,- матриця Якоби системи функцій
,- матриця Якоби системи функцій 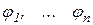 . Припускаючи, що
. Припускаючи, що 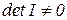 , розв'яжимо останнє рівняння відносно x. Тоді
, розв'яжимо останнє рівняння відносно x. Тоді
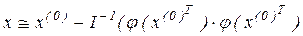
і на основі цього співвідношення формується обчислювальний процес
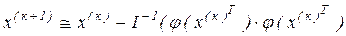 , (5.5) , (5.5)
|
який і називається методом Ньютона.
Якщо послідовність 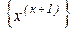 сходиться до деякого вектора x, то він очевидно, і є рішенням системи (5.41). Дійсно, у цьому випадку з (5.5) треба
сходиться до деякого вектора x, то він очевидно, і є рішенням системи (5.41). Дійсно, у цьому випадку з (5.5) треба
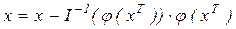 ,
,
звідки, у силу 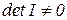 ,
, 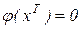 .
.
Питання збіжності послідовності (5.5) можуть бути вивчені також, як у п. 5.2. Достатнім для реалізації методу в області D, що містить рішення, є вимога 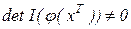 .
.
 2015-08-21
2015-08-21 195
195







