На рис. 1 изображен последовательный колебательный контур, состоящий из конденсатора, соленоида и резистора. Цель данной работы - изучение явления резонанса в колебательном контуре под действием внешней синусоидальной электродвижущей силы звуковой частоты.
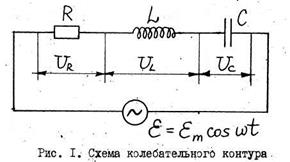
Рассмотрим процессы, происходящие в цепи, изображенной на рис. 1. При наличии переменной ЭДС с амплитудой 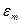
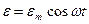 (1)
(1)
в цепи возникнет переменный ток той же циклический (круговой) частоты  (
(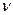 -частота), что и приложенная ЭДС, но с некоторым сдвигом по фазе
-частота), что и приложенная ЭДС, но с некоторым сдвигом по фазе
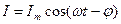 (2)
(2)
Переменный ток вызовет на всех элементах цепи - резисторе сопротивлением R, соленоиде индуктивностью L, конденсаторе ёмкостью С, соответствующие падения напряжения 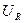 ,
, 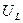 и
и 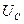 .
.
Напряжение на резисторе определяется законом Ома и равно:
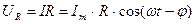 (3)
(3)
Сдвиг фаз между колебаниями 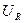 и I, как видно из сравнения формул (2) и (3), равен нулю.
и I, как видно из сравнения формул (2) и (3), равен нулю.
Переменный ток, текущий через соленоид индуктивностью L вследствие явления самоиндукции вызовет ЭДС самоиндукции
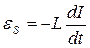
Если считать индуктивность идеальной, т.е. активное сопротивление соленоида равным нулю, то в соответствии с законом Ома для участка, цепи, содержащего ЭДС, 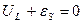 . Напряжение на соленоиде
. Напряжение на соленоиде 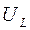 при этом будет равно ЭДС самоиндукции с обратным знаком, то есть;
при этом будет равно ЭДС самоиндукции с обратным знаком, то есть;
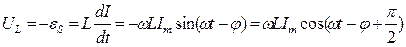 (4)
(4)
Как видно из (2) и (4), напряжение на соленоиде 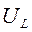 опережает по фазе силу тока I на
опережает по фазе силу тока I на 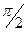 . Величина
. Величина 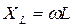 называется реактивным индуктивным сопротивлением, причем из (4)
называется реактивным индуктивным сопротивлением, причем из (4)
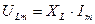 , где амплитуда колебаний напряжения на соленоиде.
, где амплитуда колебаний напряжения на соленоиде.
Протекание переменного тока через конденсатор ёмкости С можно трактовать как непрерывную перезарядку конденсатора, т.е. непрерывное изменение во времени заряда q на конденсаторе
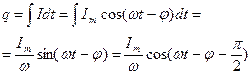 (5)
(5)
При этом напряжение на конденсаторе, как известно, определяется отношением заряда конденсатора к его ёмкости:
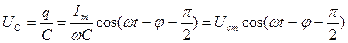 (6)
(6)
Величина 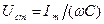 является амплитудой напряжения на конденсаторе. Величина
является амплитудой напряжения на конденсаторе. Величина 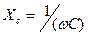 называется реактивным емкостным сопротивлением, причём из (6)
называется реактивным емкостным сопротивлением, причём из (6) 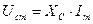 . Из формулы (2) и (6) видно, что напряжение на конденсаторе UC отстаёт по фазе от силы тока I на
. Из формулы (2) и (6) видно, что напряжение на конденсаторе UC отстаёт по фазе от силы тока I на 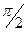 .
.
По второму закону Кирхгофу для схемы, изображений на рисунке 1,
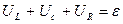
или
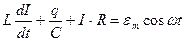 (7)
(7)
Продифференцировав уравнение (7) по времени, получим
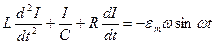 (8)
(8)
или
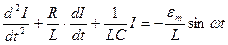 (9)
(9)
Введя в уравнение (9) коэффициенты затухания 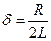 и частоту собственных колебаний
и частоту собственных колебаний 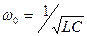 , получим дифференциальное уравнение вынужденных колебаний
, получим дифференциальное уравнение вынужденных колебаний
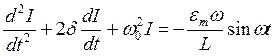 (10)
(10)
Решением этого дифференциального уравнения является
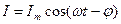 , где
, где
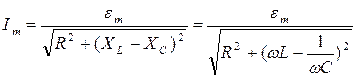 (11)
(11)
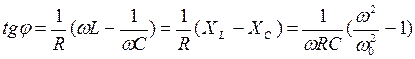 (12)
(12)
Величина 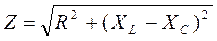 называется полным сопротивлением цепи;
называется полным сопротивлением цепи;
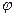 - сдвиг колебаний между колебаниями внешний ЭДС и силой тока в цепи. Ток отстает от напряжения
- сдвиг колебаний между колебаниями внешний ЭДС и силой тока в цепи. Ток отстает от напряжения 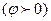 или опережает его
или опережает его 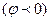 в зависимости от соотношения между
в зависимости от соотношения между 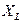 и
и 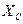 . Если частота изменения ЭДС
. Если частота изменения ЭДС 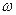 равна частоте собственных колебаний тока в контуре (
равна частоте собственных колебаний тока в контуре (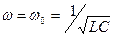 ), то
), то 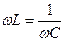 . При этом
. При этом 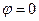 , то есть изменения тока и ЭДС происходят в фазе. В этом случае полное сопротивление Z становится минимальным и равным R, а амплитуда колебаний силы тока в цепи принимает максимальное значение. Напряжение на конденсаторе
, то есть изменения тока и ЭДС происходят в фазе. В этом случае полное сопротивление Z становится минимальным и равным R, а амплитуда колебаний силы тока в цепи принимает максимальное значение. Напряжение на конденсаторе 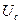 и на соленоиде
и на соленоиде 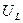 становится одинаковыми по амплитуде и противоположными по фазе (
становится одинаковыми по амплитуде и противоположными по фазе (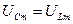 ).
).
Рассмотренное явление называется резонансом токов. Из (11) следует, что амплитудное значение тока при резонансе 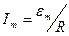 . Амплитудное значение напряжения на конденсаторе при резонансе равно
. Амплитудное значение напряжения на конденсаторе при резонансе равно
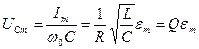 (13)
(13)
Здесь 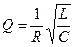 добротность контура. Если Q>1, то при резонансе напряжения на соленоиде и на конденсаторе превышает в Q раз ЭДС
добротность контура. Если Q>1, то при резонансе напряжения на соленоиде и на конденсаторе превышает в Q раз ЭДС 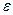 , приложенную к цепи.
, приложенную к цепи.
Отметим, что максимум амплитуды колебаний силы тока достигается при частоте 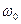 , а максимум амплитуды колебаний напряжения на конденсаторе (резонанс напряжений) – при частоте
, а максимум амплитуды колебаний напряжения на конденсаторе (резонанс напряжений) – при частоте 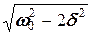 , несколько меньшей
, несколько меньшей 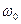 . Однако если
. Однако если 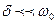 или
или
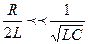 ,
,
то это различие несущественно.
 2015-08-21
2015-08-21 783
783








