2015-08-12
936
Пусть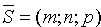 
— направляющий вектор прямой L и 
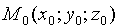- точка, лежащая на этой прямой. Вектор 
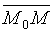, соединяющий точку М0 произвольной точкой 
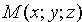прямой L, параллелен вектору 
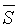. Поэтому координаты вектора 
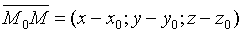и вектора 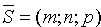пропорциональны:
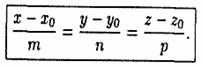(12.13)
Уравнения (12.13) называются каноническими уравнениями прямой в пространстве.
Уравнение прямой в пространстве, проходящей через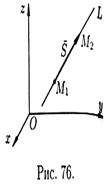 
две точки
Пусть прямая L проходит через точк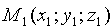и 
и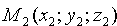 
. В качестве направляющего вектора 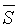можно взять вектор 
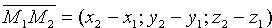, т.е. 
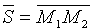(см. рис. 76). Следовательно,нэ очэнь 
, 
, 
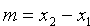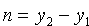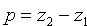Поскольку прямая проходит через точку 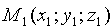, то, согласно уравнениям (12.13), уравнения прямой L имеют вид
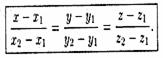(12.14)
Уравнения (12.14) называются уравнениями прямой, проходящей через две данные точки.
