2015-08-12
560
Пусть имеем функцию 2-х переменных z = f (x, y). Частные производные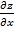 
= 
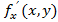и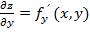 
тоже могут быть функциями двухпеременных х и у. Поэтому от них снова можно находить частные производные. Эти частные производные обозначаются символами:
; 
;
; 
.
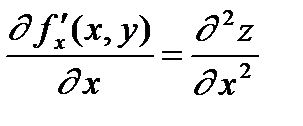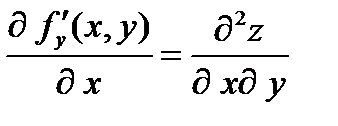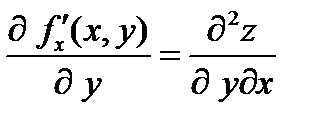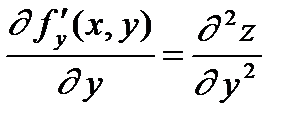Порядок дифференцирования функции двух переменных:
 = 
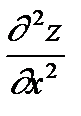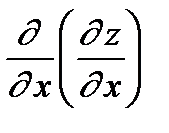
| – f (x, y) дифференцируется последовательно два раза по х при фиксированном y. |
  = 
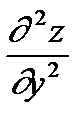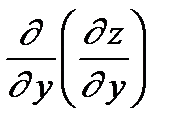
| – f (x, y) дифференцируется последовательно два раза по у при фиксированном x. |
 = 
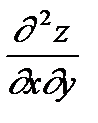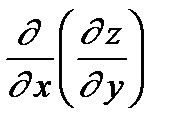
| – Смешанная производная: f (x, y) дифференцируетсясначала по y (x фиксировано), а потом результат– по x (y фиксировано). |
Можно показать, что если функция z = f (x, y) имеет непрерывные смешанные производные, то эти производные равны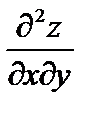 
= 
.
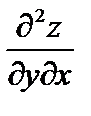От производных второго порядка снова можно вычислять частные производные по х и по у, получим производные третьего порядка и т.д. Частная производная (n)-го порядка есть первая производная от производной (n- 1)-го порядка.
