Как и для функции одной переменной, для функции двух переменных можно дать геометрическую интерпретацию производной в точке.
Рассмотрим произвольную точку А (х 0, у 0, z 0) графика функции z = f (x, y) (рис.9). Проведем сечения графика плоскостями у=у 0 и x=х 0, параллельными координатным x 0 z и y 0 z. В сечениях получим кривые AM и AN. Проведем касательные AS и AT к этим кривым через точку А.
Частная производная 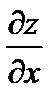 функции z = f (x, y) в точке (х 0, у0) численно равна тангенсу угла наклона касательной AS:
функции z = f (x, y) в точке (х 0, у0) численно равна тангенсу угла наклона касательной AS: 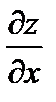 = t gb.
= t gb.
Частная производная 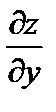 в точке (х 0, у 0) численно равна тангенсу угла наклона касательной AT:
в точке (х 0, у 0) численно равна тангенсу угла наклона касательной AT: 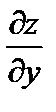 =t ga.
=t ga.
Примеры Найти частные производные следующих функций:
1. z = x 2+ y. Частные производные: 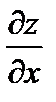 =2 x;
=2 x; 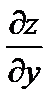 = 1.
= 1.
2. z = x 2sin y. Частные производные: 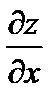 =2 x sin y;
=2 x sin y; 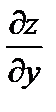 = x 2cos y.
= x 2cos y.
3. 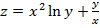 . Частные производные:
. Частные производные: 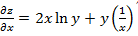 =
= 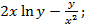
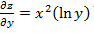
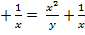 .
.
 2015-08-12
2015-08-12 765
765








