Критерии проверки параметрических и непараметрических гипотез: t-критерий, F –критерий, критерий согласия Пирсона, критерий согласия Колмогорова (самостоятельно)

Пусть даны выборка X = (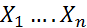) из неизвестного совместного распределения 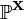, и семейство статистических гипотез 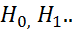. Тогда статистическим критерием называется функция, устанавливающая соответствие между наблюдаемыми величинами и возможными гипотезами: f: .

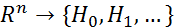Таким образом каждой реализации выборки 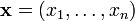статистический критерий сопоставляет наиболее подходящую с точки зрения этого критерия гипотезу о распределении, породившем данную реализацию.

Критерий Пирсона Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H ₀ о том, что эта случайная величина подчиняется закону распределения F (x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F ^* (x) исследуемой случайной величины. Сравнение эмпирического распределения F ^* (x) и теоретического (или, точнее было бы сказать, гипотетического - т.е. соответствующего гипотезе H ₀) распределения F (x) производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона. Для проверки критерия вводится статистика:

;

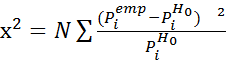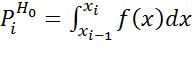
где 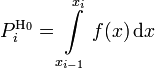— предполагаемая вероятность попадения в i -й интервал, 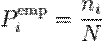— соответствующее эмпирическое значение, n_i — число элементов выборки из i -го интервала, N — полный объём выборки. Также используется расчет критерия по частоте, тогда:

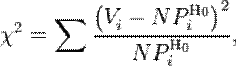
где V_i - частота попадания значений в интервал. Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ².