2015-08-12
725
Пусть имеется выборка Х1…Хn в соответствии N признака Х, и пусть требуется проверить гипотезу о том, что доля признака ГС= предполагаемому значению Rо
1. Вызов.гипотезу Ho:Р=Ro
p=Ro где Р-доля пр-ка в ГС.
2.Ні= p<Ro Ro-предполаг. значение
p>Ro доли признака в ГС
3.Экпер. значение стат-ки определяется формулой
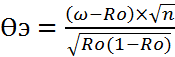,где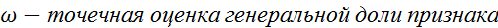 
.
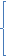4. Ф(Ѳкр)=1-α= 
Н1:Р≠Ro
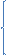Ѳэ= Ф(Ѳкр)=1-2α Н1:Р>Ro
p<Ro
Tα,v=Тα,n-1 Н1: Р≠Ro
Tα,v=Tα,n-1 h1: Р>Ro
p<Ro
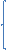5. 
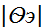= ≤Ѳкр Но: Н/отверг.
>Ѳкр Но: отверг. И прин. Н1
34. Проверка гипотезы о равенстве средних значений двух нормальных ГС.
Пусть из 2 ГС V-ми №1 и №2 извлечены 2 выборки n1 и n2 знач. Х1….Хn1=Y1….Yn2 норм. Распред. Признака Х в I ГС, Y во II ГС.
проверим гипотезу о том, что ген.ср=между собой
1. Но=Х=Y, Н1: Х≠Y
X>Y гдеХ и Y – ср.знач.призн.Хи Yв ГС.
X<Y
2. Задано таблицей
3. Экспер.знач.стат-ки крит.
Ѳэ=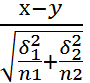 
в случае, если дисперсии известны И=соответственно
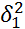и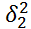 
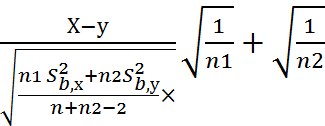в случае если дисперсии Гс не известны
35. Проверка гипотезы о равенстве дисперсий двух нормал ГС.
пусть из 2 ГС V-ами №1 и №2 извлечены выборки n1 и n2 нормально распределенных в ГС. Пусть по данным найдены выб-е значения дисперси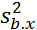й 
и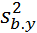 
.
проверим гипотезу о равенстве дисперсий:
1. Но: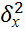 
= 
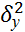, Н1: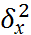 
≠ 
> 
<
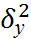
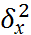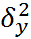
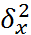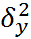
2. Ѳэ=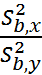 
, если 
> 
|
|
|
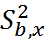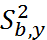
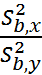, если <
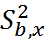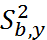
3. Ѳкр=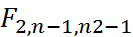 
>
<
, 
, 
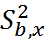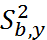
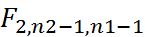
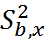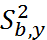
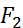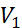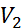- квинтиль Фишера-Снедекора, в таблице приложения.
36. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
37. Проверка гипотезы о показательном распределении генеральной совокупности с помощью критерия Пирсона.
38. Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Пирсона.
Проверка гипотезы о нормальном распределении признака в ГС
Схема проверки:
1о. Выдвигается гипотеза Но: признак Х в ГС распределён по нормальному закону, и альтернативная гипотеза Н1: признак в ГС распределён по другому, отличному от нормального, закону распределения.
2о. Вычисляются теоретические вероятности
pi’ = P(xi ≤ X ≤ xi+1)=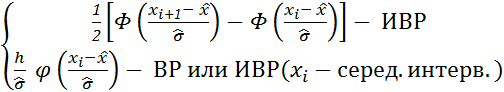 
· Φ(х) – ненормальная функция Лапласа.
· φ(х) – малая функция Лапласа, значение даны в приложениях учебника.
· h – разница между двумя соседними вариантам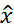и.
· 
и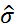 
- несмещённые точечные оценки генерального среднего и генерального сред. квадратич. отклонения, опред. равенством: 
; 
.
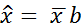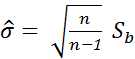3o. Вычисляются теоретические частоты по формуле: ni’ = pi’ n
4o. Находится экспериментальное значение статистики критерия по формуле
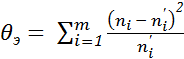, где
· m – число вариант (интервалов).
· ni – эксперемент. частоты, заданные в ВР или ИВР
5о. Находится при заданном уровне значимости α критическое значение статистики критерия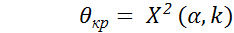 
, где
· k – число степеней свободы распределения: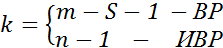 
.
|
|
|
· S – число параметров проверяемого закона распределения (при S = 2).
6o. Сравнивается эксперемент. и критическ. значения статистики и делается соответствующий статистический вывод:
.
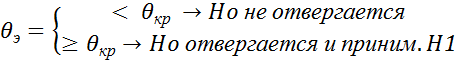Примечания:
1о. По аналогичной схеме провер. гипотеза о распределении признака в ГС по другим законам, находясь при этом, теоретические частоты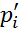 
соответствуют формулам проверяемого закона: 
=
· 
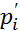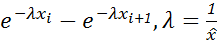при проверке распред. признака в ГС по показательному закону
· 
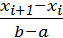– по равномерному закону
· 
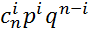– по биномиальному закону
· 
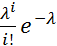– по закону Пуассона
2о. При проверке распред. признаков в ГС по нормальному закону интервалы с частотами, меньшими 5 объединяются с соседними.
3о. Критерий является приближённым и применим при объёмах выборки ≥30, а лучше ≥50.
