Регрессия – средн изменение результативного признака, приходящееся на единицу изменения факторного признака, а функция, отображающая связь между признаками, называется уравнением регрессии.
Регрессионн. анализ служит для опред вида связи между результирующим или факторным признаком и дает возможность прогнозировать значения результ. признака по знач независимых факторн. призн.
Модели регрессии: парная и множественная регрессии. Уравнение регрессии, отображающее зависимость результативного признака лишь от 1го факторного – уравнение парной регрессии, а отображающая зависимость результирующего признака от двух и более факторных – уравнение множественной регрессии.
Парная линейная регрессия – линейная связь между двумя переменными Х и У (описывается в виде прямой), уравнение 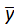 = aх + b
= aх + b
Метод наименьших квадратов. Суть метода наим квадратов заключается в выборе такой линии регрессии, чтобы сумма квадратов отклонений по вертикали между точками и этой линией была бы минимальной:
Схема: 1. Сумма квадратов отклонений S(a, b) экспериментальных значений признака У, от значений данного признака, получаем из уравнения регрессии: 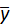 x,i=ахi=и
x,i=ахi=и
S (a, b)= 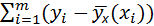 2 <=> S (a, b)=
2 <=> S (a, b)= 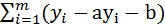 2
2
2. Находятся частные производные по а и b от реальной данной суммы квадратов отклонений:
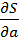 =
= 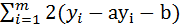 *(-xi)
*(-xi)
(Um)´= mum-1
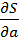 =
= 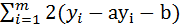 *(-1)
*(-1)
3. Система уравнений относительно а и b приравниваем данные производных к 0:
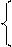
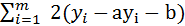 *(-xi)=0
*(-xi)=0
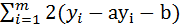 *(-1)=0
*(-1)=0
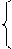 a
a 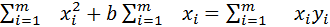
a 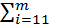 xi + bm =
xi + bm = 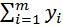
Решение полученная система, относительно а и b.
a = rb* 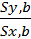 , b=
, b= 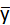 b -
b - 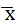 b*rb*
b*rb* 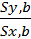
Подставляются найденные значения а и b в искомое уравнение регрессии и принимает вид: 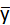 x=rb*
x=rb* 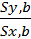 (x-
(x- 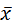 b)+
b)+ 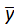 b
b
 2015-08-12
2015-08-12 255
255








