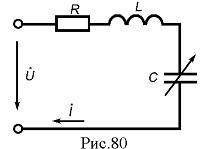
Резонансу можна досягти не тільки зміною частоти напруги живлення, але й зміною індуктивності або ємності. Припустимо, що у послідовному контурі може змінюватись ємність (рис.80). Струм контуру дорівнює:
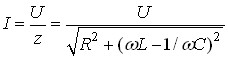 .
.
Якщо 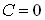 , то
, то 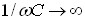 , а
, а 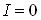 . Зі зростанням ємності С її реактивний опір
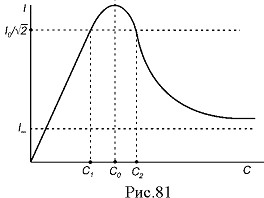
. Зі зростанням ємності С її реактивний опір 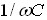 спадає, а струм I – зростає. Коли
спадає, а струм I – зростає. Коли 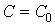 , стум досягає свого найбільшого значення
, стум досягає свого найбільшого значення 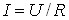 . З подальшим зростанням ємності реактивний опір (
. З подальшим зростанням ємності реактивний опір (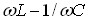 ) також зростає (а отже й повний опір
) також зростає (а отже й повний опір 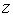 ), а струм – спадає. Якщо С??, то
), а струм – спадає. Якщо С??, то 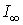 досягає значення:
досягає значення:
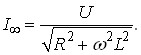
Добротність контуру:
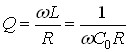 .
.
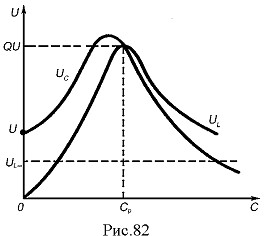
Напруга на індуктивності 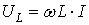 . Так як
. Так як 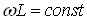 , то UL буде повторювати форму струму (рис.82). Максимальне значення:
, то UL буде повторювати форму струму (рис.82). Максимальне значення:
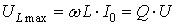 .
.
Якщо 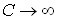 , то
, то
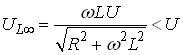
Напруга на ємності:
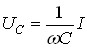 .
.
Якщо 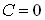 , то
, то 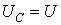 .
.
При зростанні ємності напруга UC також зростає і досягає свого максимального значення при С<C0 (при Q>1).
При С=C0:
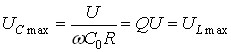 .
.
З подальшим зростанням С (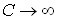 ) UC спадає до 0.
) UC спадає до 0.
Якщо Q>10, то можна вважати, що максимальна напруга на ємності дорівнює максимальній напрузі на індуктивності (похибка менше 1%):
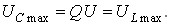
Вимірявши значення ємностей С1 та С2, при яких струм у 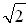 раз менше за резонансне значення, можна розрахувати параметри кола R, L, Q з рівняння:
раз менше за резонансне значення, можна розрахувати параметри кола R, L, Q з рівняння:
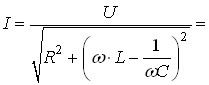
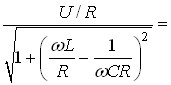
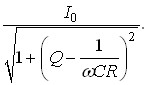
Якщо 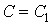 , або
, або 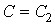 підкорінний вираз дорівнює
підкорінний вираз дорівнює 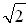 , тобто:
, тобто:
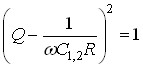 .
. 
Звідси отримуємо вирази:
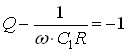 ;
; 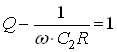 (*)
(*)
Якщо відняти від першого виразу другий будемо мати:
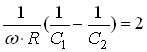 або
або 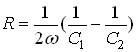 . (**)
. (**)
Якщо додати перше та друге співвідношення (*) то отримаємо:
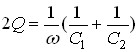 .
.
Підставляємо у цей вираз (**):
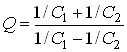 .
.
Тоді індуктивність контуру:
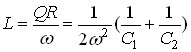 .
.
Резонанс у індуктивно зв'язаних контурах
Для підвищення крутизни резонансних характеристик (покращання вибіркових якостей) використовують двоконтурні резонансні кола: два резонансних контури, кожний з яких окремо налагоджений на одну й ту саму частоту. Контури можуть бути зв'язані електричне (ємністно), або індуктивно.
Розглянемо резонансні явища для випадку двох однакових послідовних контурів, які мають трансформаторний зв'язок (рис.83).
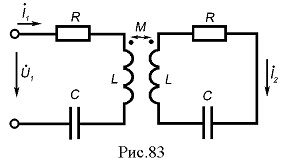
Рівняння можна записати у вигляді:
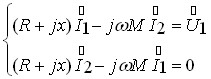 (*),
(*),
де 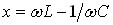 .
.
На частоті 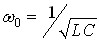 кожний контур налагоджується у резонанс
кожний контур налагоджується у резонанс 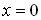 . З системи рівнянь (*) знаходимо:
. З системи рівнянь (*) знаходимо:
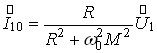 ;
; 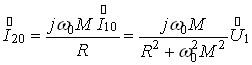 .
.
Таким чином вхідні струм та напруга співпадають по фазі (коло налаштоване у резонанс).
На всіх інших частотах 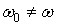 :
: 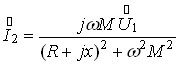 .
.
Тоді:
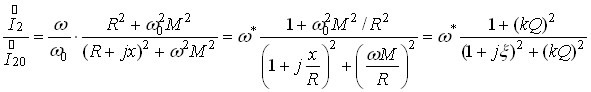 , (**)
, (**)
де 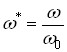 - відносна частота;
- відносна частота; 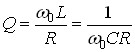 - добротність кожного з контурів;
- добротність кожного з контурів; 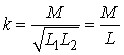 - коефіцієнт зв’язку;
- коефіцієнт зв’язку; 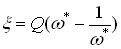 - узагальнена розстройка.
- узагальнена розстройка.
Дійсно: 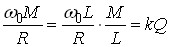 ;
;
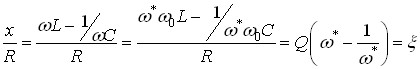 .
.
Окрім того у виразі (**) прийняте припущення, що для контуру з достатньо великою добротністю 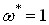 (тому
(тому 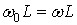 ). Це вірно при достатньо малих розстройках (так для (
). Це вірно при достатньо малих розстройках (так для (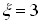 та
та 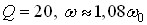 ).
).
За умови 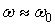 резонансна крива може бути описана виразом:
резонансна крива може бути описана виразом:
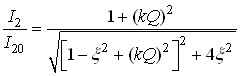 .
.
Для слабкого зв'язку 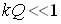 . Тоді:
. Тоді:
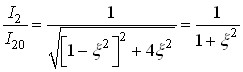 .
.
Резонансна крива має один максимум за умови 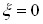 тобто
тобто 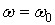 . На межах смуги пропускання
. На межах смуги пропускання 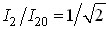 . Тоді маємо:
. Тоді маємо:
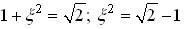 .
.
На межах смуги пропускання 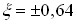 , а у послідовному контурі
, а у послідовному контурі 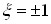 . Таким чином, за умови слабкого зв'язку, смуга пропускання зв'язаних контурів буде меншою, ніж у послідовного контуру (краща вибірковість).
. Таким чином, за умови слабкого зв'язку, смуга пропускання зв'язаних контурів буде меншою, ніж у послідовного контуру (краща вибірковість).
За умови критичного зв'язку (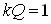 ):
):
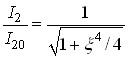 ,
,
а на межах смуги пропускання
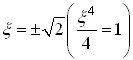 .
.
Тобто у цьому випадку смуга пропускання зв'язаних контурів буде більшою, ніж у послідовному контурі.
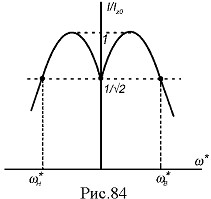
За умови сильного зв'язку 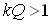 має місце резонансна крива з двома максимумами (рис.84). Смуга пропускання у 3,1 рази більша ніш у послідовному контурі при тій самій добротності контурів, а характеристика ближче до прямокутної. Це може бути досить суттєвою перевагою при побудові широкосмугових систем.
має місце резонансна крива з двома максимумами (рис.84). Смуга пропускання у 3,1 рази більша ніш у послідовному контурі при тій самій добротності контурів, а характеристика ближче до прямокутної. Це може бути досить суттєвою перевагою при побудові широкосмугових систем.
Значення резонансного струму 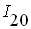 залежить від коефіцієнта зв'язку контурів і досягає максимуму за умови
залежить від коефіцієнта зв'язку контурів і досягає максимуму за умови 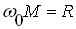 :
:
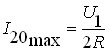 .
.
Розглянутий режим має назву «повного резонансу». При цьому настроюють кожний контур та коефіцієнт зв'язку.
Аналогічно можна провести дослідження «частинних резонансів». Перший частинний резонанс досягається зміною параметрів першого контуру (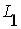 або
або 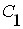 ). При цьому
). При цьому 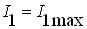 ,
, 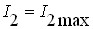 , а струм
, а струм 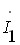 співпадає за фазою з напругою
співпадає за фазою з напругою 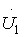
Другого частинного резонансу досягають зміною параметрів другого контуру (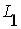 ,
, 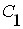 ), досягаючи максимуму струму
), досягаючи максимуму струму 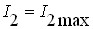 .
.
«Складний резонанс» має місце при зміні параметрів одного з контурів та коефіцієнту зв'язку.
нагору
наступний елемент курсу попередній елемент курсу
додому
Последнее изменение: Monday 14 May 2012, 15:26
Вы используете гостевой доступ (Вход)
TEK
 2015-08-12
2015-08-12 716
716







