Складаємо характеристичне рівняння даного диференціального рівняння та знаходимо його корені:
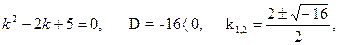
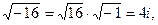
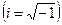 .
.
Таким чином, 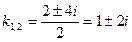 ,
, 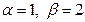 .
.
Отримуємо: 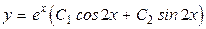 .
.
4.2. Неоднорідні лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами та спеціальною правою частиною
Неоднорідне рівняння має вигляд: 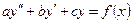 (4.4)
(4.4)
Його розв’язком y = y (x) буде сума: 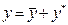 , де
, де 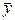 – загальний розв’язок відповідного однорідного диференціального рівняння
– загальний розв’язок відповідного однорідного диференціального рівняння 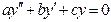 ,
, 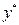 – частинний розв’язок неоднорідного рівняння (4.4), вигляд якого визначається залежно від вигляду правої частини f(x) рівняння (4.4) згідно з таблицею (4.5):
– частинний розв’язок неоднорідного рівняння (4.4), вигляд якого визначається залежно від вигляду правої частини f(x) рівняння (4.4) згідно з таблицею (4.5):
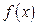
| Корені характ. рівн. | Частинний розв’язок 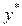
|
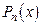
| 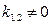
| 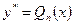 - многочлен степеня n. - многочлен степеня n.
|
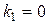
| 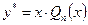
| |
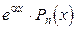
| 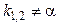
| 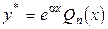
|
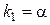
| 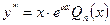
| |
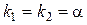
| 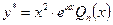
| |
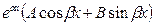
| 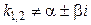
| 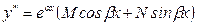
|
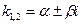
| 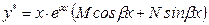
|
 2015-08-13
2015-08-13 401
401








