Знайти загальний розв’язок диференціального рівняння: 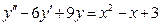 .
.
Розв’язання
1. Запишемо однорідне рівняння, яке відповідає даному диференційному рівнянню, та знайдемо його загальний розв’язок 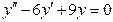 ,
, 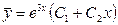 .
.
2. f(x) = 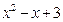 – многочлен 2-го степеня, тому частинний розв’язок
– многочлен 2-го степеня, тому частинний розв’язок 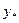 , згідно з таблицею (3.5), шукаємо у вигляді:
, згідно з таблицею (3.5), шукаємо у вигляді: 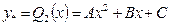 ,
,
Знаходимо коефіцієнти А, В, С.
Оскільки ліва частина даного диференціального рівняння містить першу та другу похідні 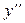 ,
, 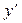 , знаходимо
, знаходимо 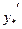 та
та 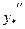 :
:
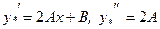 .
.
Підставимо в дане рівняння знайдені похідні та 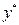 :
:
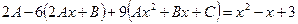 ,
,
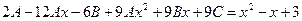 .
.
3. Якщо рівні многочлени, то рівні й коефіцієнти при однакових степенях х, тобто:
при: 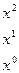
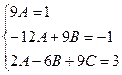 , звідки:
, звідки:
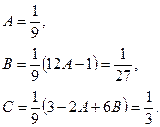
Частинний розв’язок: 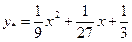 .
.
4. Загальний розв’язок 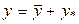 запишемо таким чином:
запишемо таким чином: 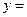
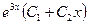 +
+ 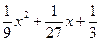 .
.
Відповідь: 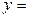
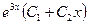 +
+ 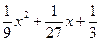 .
.
 2015-08-13
2015-08-13 427
427








